题目内容
【题目】已知函数![]() .
.
(1)当![]() 为何值时,
为何值时, ![]() 轴为曲线
轴为曲线![]() 的切线;
的切线;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,讨论
,讨论![]() 零点的个数.
零点的个数.
【答案】(1)当![]() 时,
时, ![]() 轴是曲线
轴是曲线![]() 的切线(2)当
的切线(2)当![]() 或
或![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 或
或![]() 时,
时, ![]() 有两个零点;当
有两个零点;当![]() 时,
时, ![]() 有三个零点.
有三个零点.
【解析】【试题分析】(1)先对函数求导,再运用导数的几何意义建立方程组进行分析求解;(2)先确定函数![]() 的解析式,再运用分类整合思想分类讨论函数的零点的个数问题以及对应的参数的范围:
的解析式,再运用分类整合思想分类讨论函数的零点的个数问题以及对应的参数的范围:
(1)设曲线![]() 与
与![]() 轴相切于点
轴相切于点![]() ,则
,则![]() ,即
,即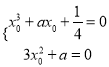 ,
,
解得: ![]() ,
,
因此,当![]() 时,
时, ![]() 轴是曲线
轴是曲线![]() 的切线;
的切线;
(2)当![]() 时,
时, ![]() ,从而
,从而![]() ,
,
∴![]() 在
在![]() 无零点,
无零点,
当![]() 时,若
时,若![]() ,则
,则![]() ,
, ![]() ,故
,故![]() 是
是![]() 的零点; 若
的零点; 若![]() ,则
,则![]() ,
, ![]() ,故
,故![]() 不是
不是![]() 的零点,当
的零点,当![]() 时,
时, ![]() ,所以只需考虑
,所以只需考虑![]() 在
在![]() 的零点个数,
的零点个数,
(Ⅰ)若![]() 或
或![]() ,则
,则![]() 在
在![]() 无零点,故
无零点,故![]() 在
在![]() 单调,而
单调,而![]() ,
,
所以当![]() 时,
时, ![]() 在
在![]() 有一个零点; 当
有一个零点; 当![]() 时,
时, ![]() 在
在![]() 无零点;
无零点;
(Ⅱ)若![]() ,则
,则![]() 在
在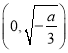 单调递减,在
单调递减,在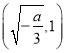 单调递增,
单调递增,
故当![]() 时,
时, ![]() 取的最小值,最小值为
取的最小值,最小值为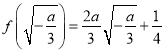 .
.
若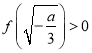 ,即
,即![]() ,
, ![]() 在
在![]() 无零点;
无零点;
若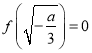 ,即
,即![]() ,则
,则![]() 在
在![]() 有唯一零点;
有唯一零点;
③若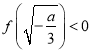 ,即
,即![]() ,由于
,由于![]() ,所以当
,所以当![]() 时,
时, ![]() 在
在![]() 有两个零点;当
有两个零点;当![]() 时,
时, ![]() 在
在![]() 有一个零点.
有一个零点.
综上,当![]() 或
或![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 或
或![]() 时,
时, ![]() 有两个零点;
有两个零点;
当![]() 时,
时, ![]() 有三个零点.
有三个零点.

练习册系列答案
相关题目