题目内容
【题目】已知数列{an}的前n项和Sn= ![]() (an﹣1),数列{bn}满足bn+2=2bn+1﹣bn , 且b6=a3 , b60=a5 , 其中n∈N*. (Ⅰ)求数列{an},{bn}的通项公式;
(an﹣1),数列{bn}满足bn+2=2bn+1﹣bn , 且b6=a3 , b60=a5 , 其中n∈N*. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=(﹣1)nbnbn+1 , 求数列{cn}的前n项和Tn .
【答案】解:(I)∵Sn= ![]() (an﹣1),∴n≥2时,an=Sn﹣Sn﹣1=
(an﹣1),∴n≥2时,an=Sn﹣Sn﹣1= ![]() (an﹣1)﹣
(an﹣1)﹣ ![]() ,化为:an=3an﹣1 . n=1时,a1=
,化为:an=3an﹣1 . n=1时,a1= ![]() ,解得a1=3.
,解得a1=3.
∴数列{an}是等比数列,首项与公比都为3.
∴an=3n .
b6=a3=33=27,b60=a5=35 .
数列{bn}满足bn+2=2bn+1﹣bn , 即bn+2+bn=2bn+1 ,
∴数列{bn}是等差数列,设公差为d,则b1+5d=27,b1+59d=243.
联立解得b1=7,d=4.
∴bn=7+4(n﹣1)=4n+3.
(II)cn=(﹣1)nbnbn+1=(﹣1)n(4n+3)(4n+7).
c2k﹣1+c2k=﹣(8k﹣1)(8k+3)+(8k+3)(8k+7)=48k+18.
∴n=2k(k∈N*)时,数列{cn}的前n项和Tn=T2k=(c1+c2)+(c3+c4)+…+(c2k﹣1+c2k)
=48×(1+2…+k)+18k= ![]() +18k=24k2+42k=6n2+21n.
+18k=24k2+42k=6n2+21n.
n=2k﹣1时,T2k﹣1=T2k﹣2+c2k﹣1=6(n﹣1)2+21(n﹣1)﹣(8k﹣1)(8k+3)=6(n﹣1)2+21(n﹣1)﹣(4n+3)(4n+7)=﹣10n2﹣31n﹣36.
∴Tn= ![]() .
.
【解析】(I)Sn= ![]() (an﹣1),可得n≥2时,an=Sn﹣Sn﹣1 , 化为:an=3an﹣1 . n=1时,a1=
(an﹣1),可得n≥2时,an=Sn﹣Sn﹣1 , 化为:an=3an﹣1 . n=1时,a1= ![]() ,解得a1 . 利用等比数列的通项公式可得an . b6=a3=33=27,b60=a5=35 . 数列{bn}满足bn+2=2bn+1﹣bn , 即bn+2+bn=2bn+1 , 利用等差数列通项公式即可得出.(II)cn=(﹣1)nbnbn+1=(﹣1)n(4n+3)(4n+7).计算c2k﹣1+c2k , 对n分类讨论即可得出.
,解得a1 . 利用等比数列的通项公式可得an . b6=a3=33=27,b60=a5=35 . 数列{bn}满足bn+2=2bn+1﹣bn , 即bn+2+bn=2bn+1 , 利用等差数列通项公式即可得出.(II)cn=(﹣1)nbnbn+1=(﹣1)n(4n+3)(4n+7).计算c2k﹣1+c2k , 对n分类讨论即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系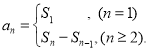 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

