题目内容
已知二次函数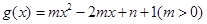 在区间
在区间 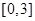 上有最大值
上有最大值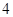 ,最小值
,最小值 .
.
(1)求函数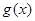 的解析式;
的解析式;
(2)设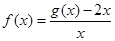 .若
.若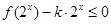 在
在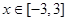 时恒成立,求
时恒成立,求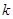 的取值范围.
的取值范围.
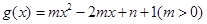 在区间
在区间 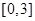 上有最大值
上有最大值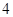 ,最小值
,最小值 .
.(1)求函数
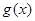 的解析式;
的解析式;(2)设
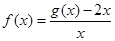 .若
.若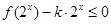 在
在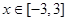 时恒成立,求
时恒成立,求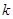 的取值范围.
的取值范围.(1)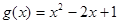 ;(2)
;(2)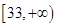 .
.
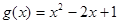 ;(2)
;(2)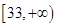 .
.试题分析:(1)根据二次函数的最值建立方程组,即可求函数
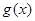 的解析式;(2)将
的解析式;(2)将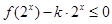 在
在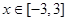 时恒成立进行转化为求函数最值,即可求出
时恒成立进行转化为求函数最值,即可求出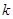 的取值范围.求最值时考虑利用换元当将函数转化为求二次函数在一个闭区间上的最值.
的取值范围.求最值时考虑利用换元当将函数转化为求二次函数在一个闭区间上的最值.试题解析:(1)∵
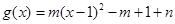 ,
,∴函数
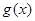 的图象的对称轴方程为
的图象的对称轴方程为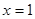 .
. 依题意得
依题意得 ,即
,即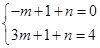 ,解得
,解得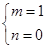 ,
,∴
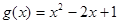 .
.(2)∵
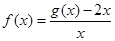 ,∴
,∴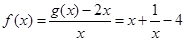 .
.∵
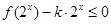 在
在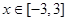 时恒成立,即
时恒成立,即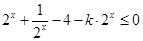 在
在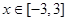 时恒成立,
时恒成立,∴
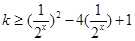 在
在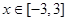 时恒成立,
时恒成立,只需
 .
.令
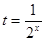 ,由
,由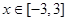 得
得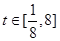
设
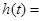
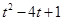 ,
,∵
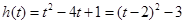 ,
,∴函数
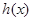 的图象的对称轴方程为
的图象的对称轴方程为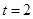 .
.当
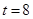 时,取得最大值
时,取得最大值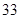 .
.∴
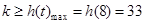 ∴
∴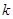 的取值范围为
的取值范围为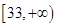 .
.
练习册系列答案
相关题目
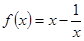 ,对任意
,对任意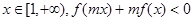 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )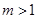
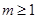
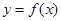 是定义域为
是定义域为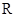 的偶函数.当
的偶函数.当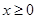 时,
时,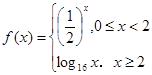 若关于
若关于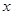 的方程
的方程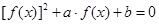
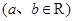 有且只有7个不同实数根,则
有且只有7个不同实数根,则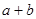 的值是.
的值是. ,
,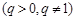 ;②
;② ;③
;③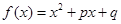 .
.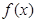 与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足
与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足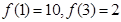 ,则
,则 (
(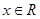 ),则( )
),则( )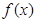 必是偶函数
必是偶函数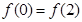 时,
时,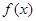 的图象必须关于
的图象必须关于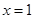 直线对称;
直线对称;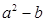
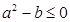 ,则
,则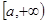 上是增函数;
上是增函数;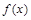 满足
满足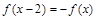 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )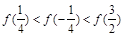
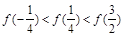
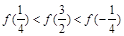
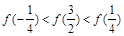
 的定义域为
的定义域为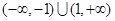 ,其图象上任一点
,其图象上任一点 满足
满足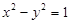 ,则给出以下四个命题:
,则给出以下四个命题: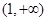 单调递增; ④若
单调递增; ④若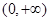
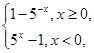 则该函数为( )
则该函数为( )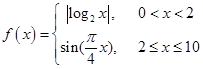 ,若存在实数
,若存在实数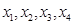 满足
满足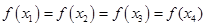 ,且
,且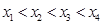 ,则
,则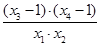 的取值范围( )
的取值范围( )