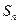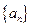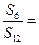题目内容
已知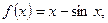 数列
数列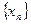 满足
满足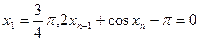
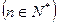
(Ⅰ) 判断并证明函数f(x)的单调性;
(Ⅱ) 设数列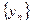 满足
满足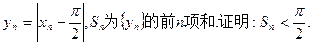
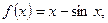 数列
数列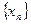 满足
满足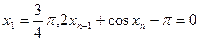
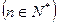
(Ⅰ) 判断并证明函数f(x)的单调性;
(Ⅱ) 设数列
 满足
满足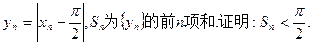
(1)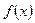 是R上的递增函数。(2)见解析
是R上的递增函数。(2)见解析
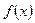 是R上的递增函数。(2)见解析
是R上的递增函数。(2)见解析(Ⅰ) 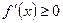 且仅当
且仅当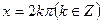 时,
时,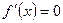 故
故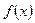 是R上的递增函数。
是R上的递增函数。
(Ⅱ) 显然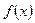 为奇函数,
为奇函数,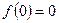 由(Ⅰ)知,当
由(Ⅰ)知,当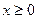 时,
时,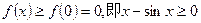
所以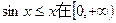 上恒成立。
上恒成立。
由已知得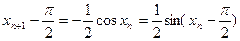
所以
所以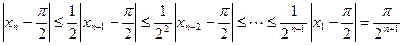
故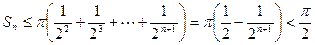
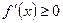 且仅当
且仅当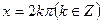 时,
时,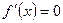 故
故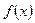 是R上的递增函数。
是R上的递增函数。(Ⅱ) 显然
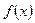 为奇函数,
为奇函数,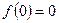 由(Ⅰ)知,当
由(Ⅰ)知,当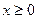 时,
时,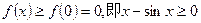
所以
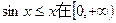 上恒成立。
上恒成立。由已知得
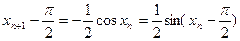
所以

所以
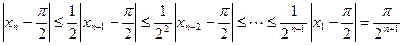
故
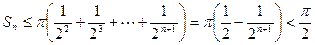

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
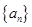 是公差为d的等差数列,
是公差为d的等差数列,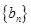 是公比为q的等比数列。
是公比为q的等比数列。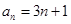 ,是否存在
,是否存在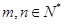 ,有
,有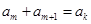 ?请说明理由;
?请说明理由;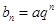 (a、q为常数,且aq
(a、q为常数,且aq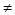 0)对任意m存在k,有
0)对任意m存在k,有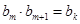 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;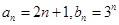 试确定所有的p,使数列
试确定所有的p,使数列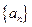 的各项都是正数,
的各项都是正数,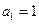 ,
,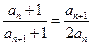 ,
,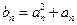 .
.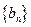 的通项公式;⑵求数列
的通项公式;⑵求数列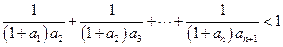 .
.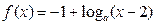 (
(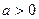 ,且
,且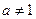 ),
),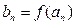 ,
, 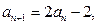 且
且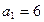 ,
,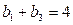
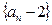 为等比数列
为等比数列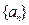 和
和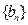 的通项公式。
的通项公式。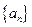 中,
中,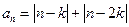 ,若对任意的正整数
,若对任意的正整数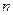 ,
,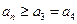 都成立,则
都成立,则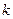 的取值范围为 。
的取值范围为 。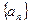 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足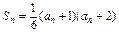 ,并且
,并且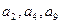 成等比数列.
成等比数列. 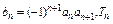 为数列
为数列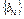 的前n项和,求
的前n项和,求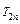 .
.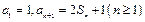
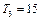 ,又
,又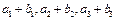 成等比数列,求Tn
成等比数列,求Tn