题目内容
已知数列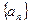 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足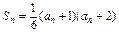 ,并且
,并且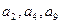 成等比数列.
成等比数列.
(I)求数列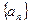 的通项公式;
的通项公式;
(II)设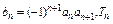 为数列
为数列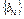 的前n项和,求
的前n项和,求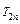 .
.
 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足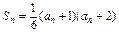 ,并且
,并且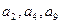 成等比数列.
成等比数列. (I)求数列
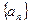 的通项公式;
的通项公式;(II)设
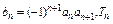 为数列
为数列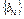 的前n项和,求
的前n项和,求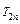 .
.(1)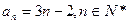 ;
;
(2)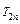
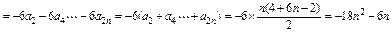
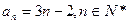 ;
;(2)
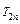
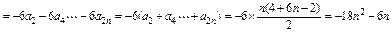
(I)∵对任意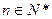 ,有
,有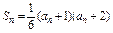 ①
①
当n≥2时,有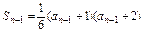 ②···
②···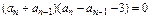
而{an}的各项均为正数,所以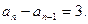
∴当n=1时,有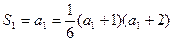 ,解得a1=1或2
,解得a1=1或2
当a1=1时,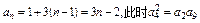 成立;
成立;
当a1=2时,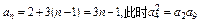 不成立;舍去.
不成立;舍去.
所以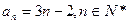
(II)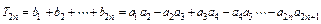
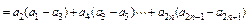
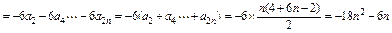
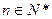 ,有
,有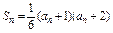 ①
①当n≥2时,有
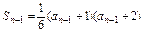 ②···
②···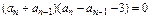
而{an}的各项均为正数,所以
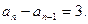
∴当n=1时,有
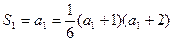 ,解得a1=1或2
,解得a1=1或2当a1=1时,
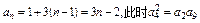 成立;
成立;当a1=2时,
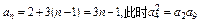 不成立;舍去.
不成立;舍去.所以
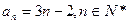
(II)
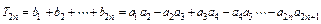
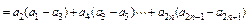
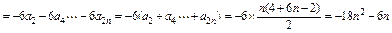

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
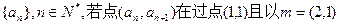 为方向向量的直线上,
为方向向量的直线上,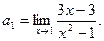 (I)求数列
(I)求数列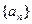 的通项公式;
的通项公式; 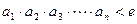 (其中e为自然对数的底数);
(其中e为自然对数的底数); 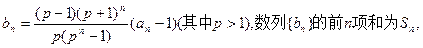
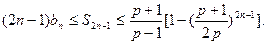
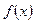 =
=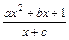 (a>0)为奇函数,且
(a>0)为奇函数,且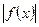 min=
min=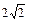 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 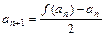 ,
,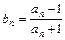 .
.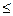
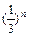 .
.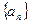 的各项均为正值,
的各项均为正值,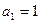 ,对任意
,对任意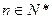 ,
,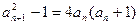 ,
,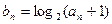 都成立.
都成立.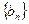 的通项公式;
的通项公式;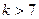 且
且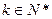 时,证明对任意
时,证明对任意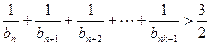 成立.
成立.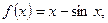 数列
数列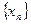 满足
满足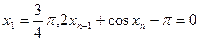
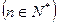
 满足
满足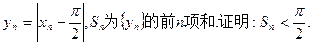
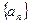 ,
,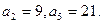
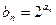 ,求数列
,求数列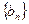 的前
的前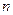 项和
项和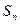 .
.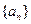
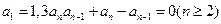
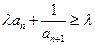 对任意
对任意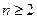 的整数恒成立,求实数
的整数恒成立,求实数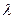 的取值范围;
的取值范围;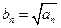 ,
,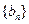 的前
的前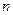 项和为
项和为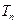 ,求证:
,求证: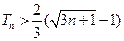
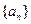 的公差
的公差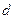 不为零,首项
不为零,首项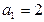 且前
且前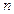 项和为
项和为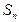 .
.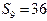 时,在数列
时,在数列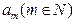 ,使得
,使得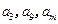 成为等比数列,求
成为等比数列,求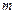 的值.
的值.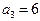 时,若自然数
时,若自然数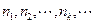 满足
满足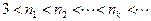 并且
并且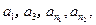
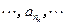 是等比数列,求
是等比数列,求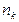 的值。
的值。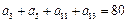 ,则a8 =( )
,则a8 =( )