题目内容
【题目】若实数![]() 满足
满足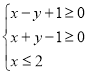 ,①
,①![]() 的最大值为________;②若
的最大值为________;②若![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是________.
的取值范围是________.
【答案】4 ![]()
【解析】
(1)首先画出可行域,和![]() 的图象,通过平移直线
的图象,通过平移直线![]() ,确定
,确定![]() 的最大值;(2)当
的最大值;(2)当![]() 时,
时,![]() 恒成立,当
恒成立,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,转化为斜率关系,利用可行域求不等式两边斜率的最值.
,转化为斜率关系,利用可行域求不等式两边斜率的最值.
首先画出可行域,令![]() ,画出初始目标函数
,画出初始目标函数![]() 的图象,
的图象,
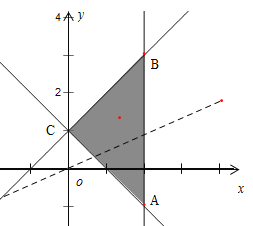
令![]() ,得
,得![]() ,当目标函数的横截距最大时,
,当目标函数的横截距最大时,![]() 也取得最大值,
也取得最大值,
所以![]() 平移至点
平移至点![]() 处,函数取得最大值,
处,函数取得最大值,
![]() ,解得:
,解得:![]() ,即
,即![]() ,代入目标函数
,代入目标函数![]() ;
;
由可行域可知![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 恒成立,
恒成立,
当![]() 时,不等式整理为:
时,不等式整理为:![]() 恒成立,
恒成立,
即![]()
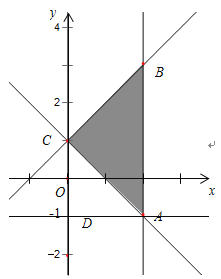
设![]() ,表示可行域内的点与定点
,表示可行域内的点与定点![]() 连线的斜率,由图象可知当定点
连线的斜率,由图象可知当定点![]() 与点
与点![]() 连结时,斜率取得最小值
连结时,斜率取得最小值![]()
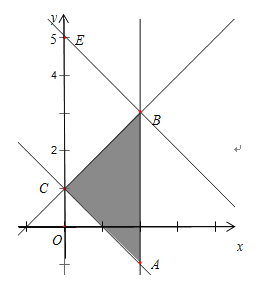
设![]() ,表示可行域内的点与定点
,表示可行域内的点与定点![]() 连线的斜率,由图象可知当
连线的斜率,由图象可知当![]() 与定点
与定点![]() 连结时,斜率取得最大值
连结时,斜率取得最大值![]()
综上可知:![]()
故答案为:4;![]()

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
