��Ŀ����
ijˮ����ֳ������һ���ǵij�����ˮ����ֳ���䣬Ϊ�˱������������Ҫ��װһЩɸ������ƽ��ͼ���£���������������£�ͼ��ʵ�߲��֣����쵥��Ϊÿ��56Ԫ��ɸ����ͼ�����߲��֣��Ľ��쵥��Ϊÿ��48Ԫ������������Ϊ160ƽ���ף����쵥��Ϊÿƽ����50Ԫ�����¼�ɸ���ĺ�Ⱥ��Բ���.
��1���ѽ�������������y��Ԫ����ʾΪ����ij�x���ף��ĺ���������������ۣ�
��2����Ҫ������ij�������15�ף���������12�ף�������ij��Ϳ���Ϊ������ʱ����ʹ�������ͣ��������ȷ��0.01�ף�

��1���ѽ�������������y��Ԫ����ʾΪ����ij�x���ף��ĺ���������������ۣ�
��2����Ҫ������ij�������15�ף���������12�ף�������ij��Ϳ���Ϊ������ʱ����ʹ�������ͣ��������ȷ��0.01�ף�

��1��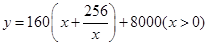 �����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
�����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
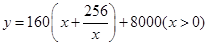 �����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
�����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������������������1����������������Ϊ�����������½����������ɸ�����������֮��. ����ij�x���� ����Ŀ�Ϊ
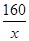 ������
������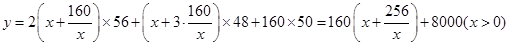 .��
.��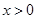 ʱ��
ʱ��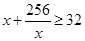 �����ҽ���
�����ҽ���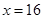 ʱȡ�Ⱥţ���ʱ
ʱȡ�Ⱥţ���ʱ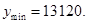 ��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ
��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ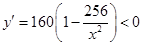 ������
������ ��
��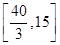 �ϵ����ݼ�����
�ϵ����ݼ�����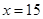 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=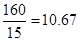 .
.������Ŀ�Ϊ
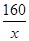 ��
��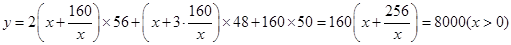 4��
4����
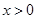 ʱ��
ʱ��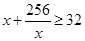 �����ҽ���
�����ҽ���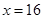 ʱȡ
ʱȡ��ʱ
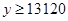
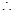 ����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8��
����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8����������
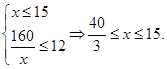 10��
10����ʱ
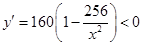 ��
�� ��
��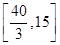 �ϵ����ݼ�����
�ϵ����ݼ�����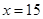 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=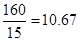 .
. ���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��
���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��
��ϰ��ϵ�д�
�����Ŀ
 ��
�� ������
������ ��
�� Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ����� ��
�� ��������
�������� ��ֱ��
��ֱ�� ��ֱ����
��ֱ���� ��ֵ��
��ֵ�� ��
�� �ϵ���Сֵ��
�ϵ���Сֵ�� ��ʹ��
��ʹ��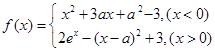 ��
��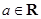 ��
��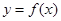 ��
��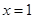 ��ȡ�ü�ֵ����
��ȡ�ü�ֵ����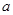 ��ֵ��
��ֵ��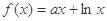 ������aΪ������
������aΪ������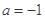 ʱ����
ʱ����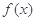 �����ֵ��
�����ֵ��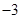 ����a��ֵ��
����a��ֵ��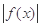 =
=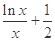 �Ƿ���ʵ���⣮
�Ƿ���ʵ���⣮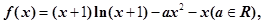
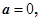 ����
����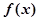 �ļ�ֵ�㼰��Ӧ�ļ�ֵ��
�ļ�ֵ�㼰��Ӧ�ļ�ֵ��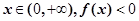 ���������ʵ��
���������ʵ��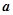 ��ȡֵ��Χ��
��ȡֵ��Χ�� (a+b-|a-b|)���������
(a+b-|a-b|)��������� ,��ô
,��ô �����ֵΪ ��
�����ֵΪ ��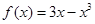 �ĵ�����������
�ĵ�����������  �ĵ�����Ϊ
�ĵ�����Ϊ ����
���� ��
��