题目内容
【题目】某地方政府欲将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场,已知AD∥BC,AD⊥AB,AD=2BC=2 ![]() 百米,AB=3百米,广场入口P在AB上,且AP=2BP,根据规划,过点P铺设两条互相垂直的笔直小路PM、PN(小路宽度不计),点M、N分别在边AD、BC上(包含端点),△PAM区域拟建为跳舞健身广场,△PBN区域拟建为儿童乐园,其他区域铺设绿化草坪,设∠APM=θ.
百米,AB=3百米,广场入口P在AB上,且AP=2BP,根据规划,过点P铺设两条互相垂直的笔直小路PM、PN(小路宽度不计),点M、N分别在边AD、BC上(包含端点),△PAM区域拟建为跳舞健身广场,△PBN区域拟建为儿童乐园,其他区域铺设绿化草坪,设∠APM=θ. 
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PN、PN进行不同风格的美化,小路PM的美化费用为每百米1万元,小路PN的美化费用为每百米2万元,试确定点M,N的位置,使得小路PM,PN的总美化费用最低,并求出最低费用.
【答案】
(1)解:∵AB=3,AP=2BP,∴AP=2,BP=1.
在Rt△PMA中,由 ![]() ,得AM=2tanθ,
,得AM=2tanθ,
∴ ![]() ,
,
∵PM⊥PN,∴∠PNB=θ,
在Rt△PNB中,由 ![]() ,得
,得 ![]() ,
,
所以 ![]() ,
,
又S梯形ABCD= ![]() (
( ![]() +2
+2 ![]() )×3=
)×3= ![]() .
.
∴绿化草坪面积S= ![]() ﹣2tanθ﹣
﹣2tanθ﹣ ![]() ,
,
连结PC,PD,

则tanθ的最大值为 ![]() =
= ![]() ,tanθ的最小值为
,tanθ的最小值为 ![]() ,
,
∴ ![]() ≤tanθ
≤tanθ ![]() ,
,
设tanθ=t,f(t)=2t+ ![]() ,则f′(t)=2﹣
,则f′(t)=2﹣ ![]() ,
,
∴当t∈[ ![]() ,
, ![]() ]时,f′(t)>0,
]时,f′(t)>0,
∴f(t)在[ ![]() ,
, ![]() ]上单调递增,
]上单调递增,
∴f(t)的最小值为f( ![]() )=
)= ![]() ,
,
∴S的最大值为 ![]() ﹣
﹣ ![]() =
= ![]() .
.
∴绿化草坪面积的最大值为 ![]() 平方百米
平方百米
(2)解:在Rt△PMA中,由 ![]() ,得
,得 ![]() ,
,
在Rt△PNB中,由 ![]() ,得
,得 ![]() ,
,
∴总美化费用为 ![]() ,由(1)可知θ∈[
,由(1)可知θ∈[ ![]() ,
, ![]() ],
],
令t=sinθ+cosθ= ![]() sin(θ+
sin(θ+ ![]() ),则t∈[
),则t∈[ ![]() ,
, ![]() ],
], ![]() ,
,
∴ ![]() ,
, 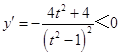 ,
,
∴ ![]() 在[
在[ ![]() ,
, ![]() ]上单调递减,
]上单调递减,
∴当t= ![]() 时,美化费用y取得最小值4
时,美化费用y取得最小值4 ![]() .
.
∴当 ![]() ,即
,即 ![]() 时,即AM=2,BM=1时总美化费用最低为4
时,即AM=2,BM=1时总美化费用最低为4 ![]() 万元.
万元.
【解析】(1)用θ表示出AM,BN,得出草坪面积S关于tanθ的函数,利用函数单调性求出最大值;(2)用θ表示出PM,PN,得出美化费用y关于θ的函数,利用换元法求出最小值.