题目内容
【题目】已知函数f(x)=(x﹣1)2+a(lnx﹣x+1)(其中a∈R,且a为常数) (Ⅰ)当a=4时,求函数y=f(x)的单调区间;
(Ⅱ)若对于任意的x∈(1,+∞),都有f(x)>0成立,求a的取值范围;
(Ⅲ)若方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根,求a的取值范围.
【答案】解:(1)函数f(x)的定义域为(0,+∞) 由 ![]() ,
,
当a=4时, ![]() ,
,
∴函数f(x)在(0,1)上单调递增,在(1,2)上单调递减,(2,+∞)在上单调递增;
(Ⅱ)由 ![]()
当a≤2时,
∵f'(x)>0对于x∈(1,+∞)恒成立,
∴f(x)在(1,+∞)上单调递增
∴f(x)>f(1)=0,此时命题成立;
当a>2时,
∵f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
∴当 ![]() 时,有f(x)<f(1)=0.这与题设矛盾,不合.
时,有f(x)<f(1)=0.这与题设矛盾,不合.
故a的取值范围是(﹣∞,2];
(Ⅱ)依题意,设g(x)=f(x)+a+1,
原题即为若g(x)在(1,2)上有且只有一个零点,求a的取值范围.
显然函数g(x)与f(x)的单调性是一致的.
当a≤0时,因为函数g(x)在(1,2)上递增,
由题意可知 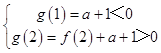 ,
,
解得 ![]() ;
;
当a>0时,因为g(x)=(x﹣1)2+alnx+(2﹣x)a+1,
当x∈(1,2)时,总有g(x)>0,此时方程没有实根.
综上所述,当 ![]() 时,方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根.
时,方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根.
【解析】(Ⅰ)根据导数和函数的单调性的关系即可求出,(Ⅱ)分类讨论,确定函数的单调性,从而解得;(Ⅲ)依题意,设g(x)=f(x)+a+1,原题即为若g(x)在(1,2)上有且只有一个零点,求a的取值范围.显然函数g(x)与f(x)的单调性是一致的,根据函数的单调性,当a<0,即可得到可知 ![]() ,解得即可,当a≥0,判断此时方程没有实根,问题得以解决.
,解得即可,当a≥0,判断此时方程没有实根,问题得以解决.

 阅读快车系列答案
阅读快车系列答案【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
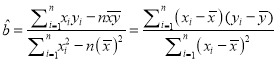 ,
, ![]() .
.