题目内容
设二次函数f(x)=x2+ax+a,方程f(x)-x=0的两根x1和x2满足0<x1<x2<1.
(1)求实数a的取值范围;
(2)试比较f(0)·f(1)-f(0)与的大小,并说明理由
(1)求实数a的取值范围;
(2)试比较f(0)·f(1)-f(0)与的大小,并说明理由
法一:(1)令g(x)=f(x)-x=x2+(a-1)x+a,
则由题意可得
?
⇒0<a<3-2.
故所求实数a的取值范围是(0,3-2).
(2)f(0)·f(1)-f(0)=g(0)g(1)=2a2,令h(a)=2a2,
∵当a>0时,h(a)单调递增,∴当0<a<3-2时,
0<h(a)<h(3-2)=2(3-2)2=2(17-12)
=2·<,即f(0)·f(1)-f(0)<.
法二:(1)同解法一.
(2)∵f(0)f(1)-f(0)=g(0)g(1)=2a2,由(1)知
0<a<3-2,
∴4a-1<12-17<0.又4a+1>0,于是
2a2-=(32a2-1)=(4a-1)(4a+1)<0,
即2a2-<0,故f(0)f(1)-f(0)<.
法三:(1)方程f(x)-x=0?x2+(a-1)x+a=0,由韦达定理得x1+x2=1-a,x1x2=a,于是0<x1<x2<1
??
?0<a<3-2.
故所求实数a的取值范围是(0,3-2).
(2)依题意可设g(x)=(x-x1)(x-x2),则由0<x1<x2<1,得f(0)f(1)-f(0)=g(0)g(1)=x1x2(1-x1)(1-x2)=[x1(1-x1)][x2(1-x2)]<22=,故f(0)f(1)-f(0)<.
则由题意可得
?
⇒0<a<3-2.
故所求实数a的取值范围是(0,3-2).
(2)f(0)·f(1)-f(0)=g(0)g(1)=2a2,令h(a)=2a2,
∵当a>0时,h(a)单调递增,∴当0<a<3-2时,
0<h(a)<h(3-2)=2(3-2)2=2(17-12)
=2·<,即f(0)·f(1)-f(0)<.
法二:(1)同解法一.
(2)∵f(0)f(1)-f(0)=g(0)g(1)=2a2,由(1)知
0<a<3-2,
∴4a-1<12-17<0.又4a+1>0,于是
2a2-=(32a2-1)=(4a-1)(4a+1)<0,
即2a2-<0,故f(0)f(1)-f(0)<.
法三:(1)方程f(x)-x=0?x2+(a-1)x+a=0,由韦达定理得x1+x2=1-a,x1x2=a,于是0<x1<x2<1
??
?0<a<3-2.
故所求实数a的取值范围是(0,3-2).
(2)依题意可设g(x)=(x-x1)(x-x2),则由0<x1<x2<1,得f(0)f(1)-f(0)=g(0)g(1)=x1x2(1-x1)(1-x2)=[x1(1-x1)][x2(1-x2)]<22=,故f(0)f(1)-f(0)<.
略

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时,
 的值;
的值; 的解析式并画出简图;
的解析式并画出简图;  的根的情况。(只需写出结果,不要解答过程).
的根的情况。(只需写出结果,不要解答过程).
 甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.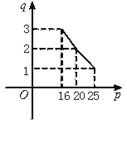
 (
( )
) 有最大值
有最大值 ,求实数a的值; (2)解不等式
,求实数a的值; (2)解不等式 (a∈R).
(a∈R).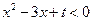 的解集为
的解集为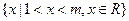 ;
; 的值;
的值;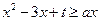 在
在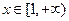 上恒成立,求实数
上恒成立,求实数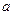 的最大值.
的最大值. 则实数a的取值( ).
则实数a的取值( ).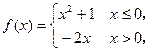 若
若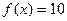 ,则
,则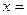
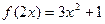 ,则函数
,则函数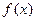 =
=  为开口向下的抛物线,且对任意x∈R都有f(1+x)=f(1-x).若向量
为开口向下的抛物线,且对任意x∈R都有f(1+x)=f(1-x).若向量 ,
,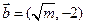 ,则满足不等式
,则满足不等式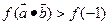 m取值范围 。
m取值范围 。