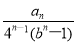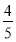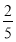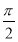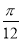题目内容
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=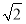 .
.
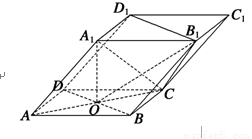
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
(1)见解析(2)θ=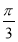
【解析】(1)法一:∵A1O⊥平面ABCD,∴A1O⊥BD.
又底面ABCD是正方形,∴BD⊥AC,又A1O∩AC=O,∴BD⊥平面A1OC,又A1C?平面A1OC,∴BD⊥A1C.
又OA1是AC的中垂线,∴A1A=A1C=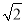 ,且AC=2,
,且AC=2,
∴AC2=AA+A1C2,
∴△AA1C是直角三角形,∴AA1⊥A1C.
又BB1∥AA1,∴A1C⊥BB1,又BB1∩BD=B,∴A1C⊥平面BB1D1D.
法二:由题设易知OA,OB,OA1两两垂直,以O为原点建立直角坐标系,如图.
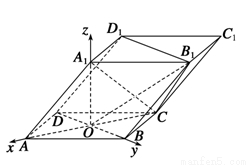
∵AB=AA1=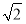 ,
,
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),
A1(0,0,1).由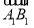 =
=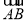 ,易得B1(-1,1,1).
,易得B1(-1,1,1).
∵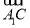 =(-1,0,-1),
=(-1,0,-1),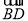 =(0,-2,0),
=(0,-2,0), =(-1,0,1).
=(-1,0,1).
∴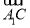 ·
·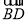 =0,
=0,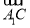 ·
·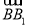 =0,
=0,
∴A1C⊥BD,A1C⊥BB1,
又BD∩BB1=B,
∴A1C⊥平面BB1D1D.
(2)设平面OCB1的法向量n=(x,y,z).
∵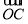 =(-1,0,0),
=(-1,0,0),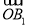 =(-1,1,1),
=(-1,1,1),
∴ ∴
∴ 取n=(0,1,-1),
取n=(0,1,-1),
由(1)知, =(-1,0,-1)是平面BB1D1D的法向量,
=(-1,0,-1)是平面BB1D1D的法向量,
∴cos θ=|cos〈n, 〉|=
〉|=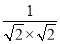 =
=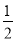 .
.
又∵0≤θ≤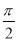 ,∴θ=
,∴θ=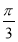 .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目