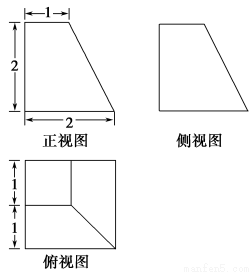
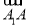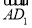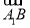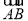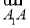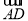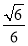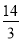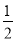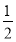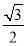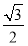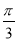题目内容
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=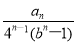 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
见解析
【解析】(1)因为点(an+1,S2n-1)在函数f(x)的图象上,所以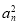 =S2n-1.
=S2n-1.
令n=1,n=2,得 即
即 解得a1=1,d=2(d=-1舍去),则an=2n-1.
解得a1=1,d=2(d=-1舍去),则an=2n-1.
由(bn-bn+1)·g(bn)=f(bn),
得4(bn-bn+1)(bn-1)=(bn-1)2.
由题意bn≠1,所以4(bn-bn+1)=bn-1,
即3(bn-1)=4(bn+1-1),所以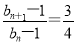
所以数列{bn-1}是以1为首项,公比为 的等比数列.
的等比数列.
(2)由(1),得bn-1=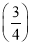 n-1.cn=
n-1.cn=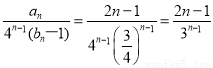 .
.
令Tn=c1+c2+c3+…+cn,
则Tn=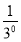 +
+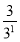 +
+ +…+
+…+ +
+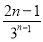 ,①
,①
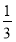 Tn=
Tn= +
+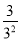 +
+ +…+
+…+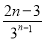 +
+ ,②
,②
①-②得,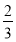 Tn=
Tn=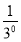 +
+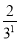 +
+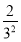 +
+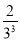 +…+
+…+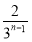 -
- =1+
=1+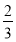 ·
·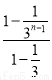 -
-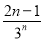 =2-
=2-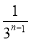 -
-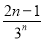 =2-
=2-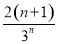 .所以Tn=3-.
.所以Tn=3-.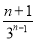
所以c1+c2+c3+…+cn=3-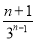 <3.
<3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目