题目内容
已知 成等比数列,且抛物线
成等比数列,且抛物线 的顶点是
的顶点是 ,
,
则 等于
等于
 成等比数列,且抛物线
成等比数列,且抛物线 的顶点是
的顶点是 ,
,则
 等于
等于 2
试题分析:由题意可知,抛物线
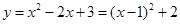 的顶点坐标为(1,2),并且由于a,b,c,d成等比数列,则必有ad=cb=2,故ad的值为2.答案为2。
的顶点坐标为(1,2),并且由于a,b,c,d成等比数列,则必有ad=cb=2,故ad的值为2.答案为2。点评:解决该试题的关键是根据等比数列性质得到bc=ad的值,然后借助于二次函数的顶点坐标进而得到结论。

练习册系列答案
相关题目
题目内容
 成等比数列,且抛物线
成等比数列,且抛物线 的顶点是
的顶点是 ,
, 等于
等于 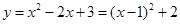 的顶点坐标为(1,2),并且由于a,b,c,d成等比数列,则必有ad=cb=2,故ad的值为2.答案为2。
的顶点坐标为(1,2),并且由于a,b,c,d成等比数列,则必有ad=cb=2,故ad的值为2.答案为2。