题目内容

3．下列函数中，图象不关于原点对称的是（　　）
A．y=ex-e-xB．y=$\frac{2}{{{e^x}+1}}$-1C．$y=ln（x+\sqrt{{x^2}+1}）$D．y=lnsinx

分析 根据函数的奇偶性判断函数是不是奇函数即可．

解答 解：若y=lnsinx，则由sinx＞0得2kπ＜x＜2kπ+π，k∈Z，定义域关于原点不对称，
则函数为非奇非偶函数，其余都为奇函数，
故选：D

点评 本题主要考查函数图象的判断，利用函数奇偶性的性质是解决本题的关键．

练习册系列答案
相关题目
13．已知F1（-c，0），F2（c，0）为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的两个焦点，若该椭圆与圆x2+y2=2c2有公共点，则此椭圆离心率的取值范围是$[\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{2}}}{2}]$．
14．下列各组中的两个函数是同一函数的是（　　）
A．f（x）=$\frac{{x}^{2}-1}{x-1}$和f（x）=x+1
B．f（r）=πr2（r≥0）和g（x）=πx2（x≥0）
C．f（x）=logaax（a＞0且a≠1）和g（x）=${a}^{lo{g}_{a}x}$（a＞0且a≠1）
D．f（x）=x和g（t）和g（t）=$\sqrt{{t}^{2}}$
11．已知函数f（x）=sin（x+θ）+$\sqrt{3}$cos（x+θ），
（1）若θ=0，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]，求f（x）的值域；
（2）若f（x）的图象关于原点对称，且θ∈（0，π），求θ的值．
18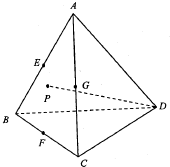．如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（　　）
A．线段FGB．线段EGC．线段EFD．线段EC
8．已知数列{an}满足an+1=2an+2n，n∈N*，a1=1，bn=$\frac{a_n}{2^n}$
（1）证明数列{bn}为等差数列．
（2）求数列{an}的通项公式an与前n项和Sn．
15．16个同类产品中有14个正品，2个次品，从中任意抽取3个，则下列事件中概率为1的是（　　）
A．三个都是正品B．三个都是次品
C．三个中至少有一个是正品D．三个中至少有一个次品
12．下列不等关系的推导中，正确的个数为（　　）
①a＞b，c＞d⇒ac＞bd②a＞b⇒$\frac{1}{a}$＜$\frac{1}{b}$③a＞b⇒an＞bn④$\frac{1}{x}$＞1⇒0＜x＜1．
A．0个B．1个C．2个D．3个
13．集合A={x|x≥1}，B={x|x＜m}，若A∪B=R，则m的最小值是（　　）
A．-1B．0C．1D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网