题目内容
7．已知各项均为正数的等比数列{an}中，a2=1，则其前3项的和S3的取值范围是（ ）| A． | （1，+∞） | B． | （0，2] | C． | （0，3] | D． | [3，+∞） |
分析 首先由等比数列的通项入手表示出S3（即q的代数式），然后利用均值不等式求出S3的范围．
解答 解：∵等比数列{an}中，a2=1，
∴S3=a1+a2+a3=a2（1+q+$\frac{1}{q}$），
∵公比q＞0时，${S}_{3}=1+q+\frac{1}{q}$≥$1+2\sqrt{q•\frac{1}{q}}$=3．
当且仅当q=1时上式等号成立．
∴前3项的和S3的取值范围是[3，+∞）．
故选：D．
点评 解本题考查等比数列前n项和的意义、等比数列的通项公式及均值不等式的应用．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18．
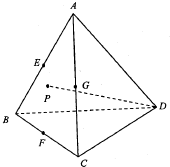如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（ ）
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（ ）| A． | 线段FG | B． | 线段EG | C． | 线段EF | D． | 线段EC |
15．16个同类产品中有14个正品，2个次品，从中任意抽取3个，则下列事件中概率为1的是（ ）
| A． | 三个都是正品 | B． | 三个都是次品 | ||
| C． | 三个中至少有一个是正品 | D． | 三个中至少有一个次品 |
12．下列不等关系的推导中，正确的个数为（ ）
①a＞b，c＞d⇒ac＞bd②a＞b⇒$\frac{1}{a}$＜$\frac{1}{b}$③a＞b⇒an＞bn④$\frac{1}{x}$＞1⇒0＜x＜1．
①a＞b，c＞d⇒ac＞bd②a＞b⇒$\frac{1}{a}$＜$\frac{1}{b}$③a＞b⇒an＞bn④$\frac{1}{x}$＞1⇒0＜x＜1．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
在一段时间内有100辆汽车经过某交通岗，有2辆汽车速度小于35km/h，有3辆汽车的速度大于75km/h，时速（单位：km/h）频率分布直方图如图所示，
17．
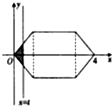如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）
如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）| A． | $\frac{11}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{29}{16}$ | D． | $\frac{33}{16}$ |