题目内容
(12分)设函数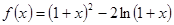 .(1)求
.(1)求 的单调区间;(2)当
的单调区间;(2)当 时,求函数
时,求函数 在区间
在区间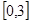 上的最小值.
上的最小值.
(1)函数的单调递增区间为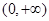 ,单调递减区间为
,单调递减区间为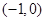 .
.
(2)当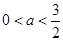 时,
时,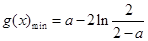 ;当
;当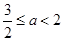 时,
时,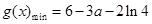
解析

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
题目内容
(12分)设函数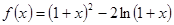 .(1)求
.(1)求 的单调区间;(2)当
的单调区间;(2)当 时,求函数
时,求函数 在区间
在区间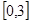 上的最小值.
上的最小值.
(1)函数的单调递增区间为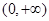 ,单调递减区间为
,单调递减区间为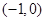 .
.
(2)当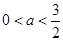 时,
时,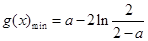 ;当
;当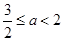 时,
时,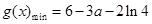
解析

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案