题目内容
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若 ,则 ,则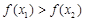 |
B
解析试题分析:∵证明y=x3是增函数时,依据的原理就是增函数的定义,
∴用演绎法证明y=x3是增函数时的大前提是:增函数的定义,
小前提是函数f(x)=x3满足增函数的定义.故选B.
考点:演绎推理的基本方法.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
将正偶数按下表排成4列:
则2 004在 ( ).
| A.第251行,第1列 | B.第251行,第2列 |
| C.第250行,第2列 | D.第250行,第4列 |
对于任意正整数n,定义“ ”如下:
”如下:
当n是偶数时, ,
,
当n是奇数时,
现在有如下四个命题:
① ;
;
② ;
;
③ 的个位数是0;
的个位数是0;
④ 的个位数是5。
的个位数是5。
其中正确的命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
用反证法证明命题:“若整系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设 都是偶数 都是偶数 |
B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 |
D.假设 至多有两个是偶数 至多有两个是偶数 |
观察下列各式: ,
, ,
, ,
, ,
, ,
, ,则
,则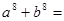 ( )
( )
| A.28 | B. | C. | D. |
已知 △ABC中,
△ABC中, ,求证:
,求证: .证明:
.证明: ∴
∴ ,其中,画线部分是演绎推理的( )
,其中,画线部分是演绎推理的( )
| A.小前提 | B.大前提 | C.结论 | D.三段论 |
下面四个判断中,正确的是( )
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+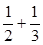 +…+ +…+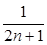 (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+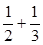 |
D.设f(x)=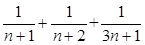 (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+ |
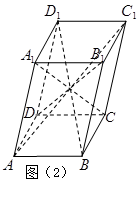
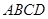 中,有
中,有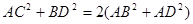 ,那么在图(2)的平行六面体
,那么在图(2)的平行六面体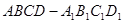 中有
中有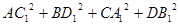 等于( )
等于( )
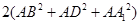
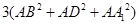

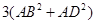
 ,则输出
,则输出 的值为 .
的值为 .