题目内容
观察下列各式: ,
, ,
, ,
, ,
, ,
, ,则
,则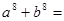 ( )
( )
| A.28 | B. | C. | D. |
B
解析试题分析:观察可得各式的值构成数列1,3,4,7,11, ,其规律为从第三项起,每项等于其前相邻两项的和,所求值为数列中的第八项.继续写出此数列为1,3,4,7,11,18,29,47,76,123, ,第十项为47,即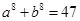 .
.
考点:归纳推理.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
下列推理中属于归纳推理且结论正确的是( )
| A.设数列﹛an﹜的前n项和为sn,由an=2n﹣1,求出s1 =12 , s2=22,s3=32,…推断sn=n2 |
B.由 cosx,满足 cosx,满足 对 对 x∈R都成立,推断 x∈R都成立,推断 为奇函数。 为奇函数。 |
C.由圆 的面积 的面积 推断:椭圆 推断:椭圆 (a>b>0)的面积s=πab (a>b>0)的面积s=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2 >23,…,推断对一切正整数n,(n+1)2>2n |
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若 ,则 ,则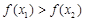 |
下面几种推理中是演绎推理的序号为( )
A.半径为 圆的面积 圆的面积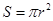 ,则单位圆的面积 ,则单位圆的面积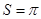 ; ; |
| B.由金、银、铜、铁可导电,猜想:金属都可导电; |
| C.由平面三角形的性质,推测空间四面体性质; |
D.由平面直角坐标系中圆的方程为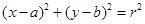 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为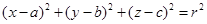 . . |
已知数列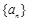 的前
的前 项和为
项和为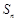 ,且
,且 ,
,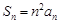
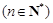 ,可归纳猜想出
,可归纳猜想出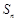 的表达式为( )
的表达式为( )
A. | B. | C.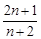 | D.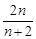 |
某个命题与自然数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得( )
| A.n=6时该命题不成立 | B.n=6时该命题成立 |
| C.n=4时该命题不成立 | D.n=4时该命题成立 |
设a,b∈R,则“a+b=1”是“4ab≤1”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
平面内有n条直线,最多可将平面分成f(n)个区域,则f(n)的表达式为( )
| A.n+1 | B.2n |
C.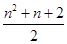 | D.n2+n+1 |
 , 编写程序求函数值(只写程序)
, 编写程序求函数值(只写程序) (只画程序框图,循环体不对不得分)
(只画程序框图,循环体不对不得分)