题目内容
已知 △ABC中,
△ABC中, ,求证:
,求证: .证明:
.证明: ∴
∴ ,其中,画线部分是演绎推理的( )
,其中,画线部分是演绎推理的( )
| A.小前提 | B.大前提 | C.结论 | D.三段论 |
A
解析试题分析:本题中应用了三角形中的大角对大边的原理,即“在三角形中,大角对大边”是“三段论”中的大前提,而“ ”是三段论中的小前提,“
”是三段论中的小前提,“ ”是三段论中的结论,故选A.
”是三段论中的结论,故选A.
考点:演绎推理中的三段论问题.

练习册系列答案
相关题目
用数学归纳法证明1+ +
+ +…+
+…+ =-
=- (
( ≠1,n∈N*),在验证n=1成立时,左边的项是( )
≠1,n∈N*),在验证n=1成立时,左边的项是( )
| A.1 | B.1+ | C.1+ + + | D.1+ + + + + |
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若 ,则 ,则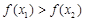 |
下面几种推理中是演绎推理的序号为( )
A.半径为 圆的面积 圆的面积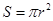 ,则单位圆的面积 ,则单位圆的面积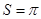 ; ; |
| B.由金、银、铜、铁可导电,猜想:金属都可导电; |
| C.由平面三角形的性质,推测空间四面体性质; |
D.由平面直角坐标系中圆的方程为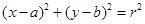 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为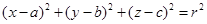 . . |
设a,b∈R,则“a+b=1”是“4ab≤1”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
平面内有n条直线,最多可将平面分成f(n)个区域,则f(n)的表达式为( )
| A.n+1 | B.2n |
C.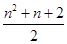 | D.n2+n+1 |
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
| A.(7,5) | B.(5,7) | C.(2,10) | D.(10,1) |
观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12 ….则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 | C.86 | D.92 |
定义平面向量之间的一种运算“☉”如下:对任意的a=(m,n),b=(p,q),令a☉b=mq-np.下面说法错误的是( )
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |