题目内容
对于任意正整数n,定义“ ”如下:
”如下:
当n是偶数时, ,
,
当n是奇数时,
现在有如下四个命题:
① ;
;
② ;
;
③ 的个位数是0;
的个位数是0;
④ 的个位数是5。
的个位数是5。
其中正确的命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
D
解析试题分析:根据条件中的描述,可以做出如下判断,
①: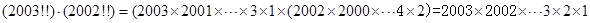 ,正确;
,正确;
②: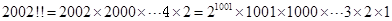 ,正确;
,正确;
③: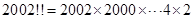 ,等号右边的因子中有末位是0的整数,显然乘积的个位数是0;正确
,等号右边的因子中有末位是0的整数,显然乘积的个位数是0;正确
④: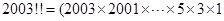 ,等号右边的因子中有末位是5的整数,显然乘积的个位数是5,正确,∴正确的命题有4个.
,等号右边的因子中有末位是5的整数,显然乘积的个位数是5,正确,∴正确的命题有4个.
考点:新定义类材料阅读题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
用数学归纳法证明1+ +
+ +…+
+…+ =-
=- (
( ≠1,n∈N*),在验证n=1成立时,左边的项是( )
≠1,n∈N*),在验证n=1成立时,左边的项是( )
| A.1 | B.1+ | C.1+ + + | D.1+ + + + + |
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且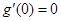 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
下列推理中属于归纳推理且结论正确的是( )
| A.设数列﹛an﹜的前n项和为sn,由an=2n﹣1,求出s1 =12 , s2=22,s3=32,…推断sn=n2 |
B.由 cosx,满足 cosx,满足 对 对 x∈R都成立,推断 x∈R都成立,推断 为奇函数。 为奇函数。 |
C.由圆 的面积 的面积 推断:椭圆 推断:椭圆 (a>b>0)的面积s=πab (a>b>0)的面积s=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2 >23,…,推断对一切正整数n,(n+1)2>2n |
推理:因为平行四边形对边平行且相等,而矩形是特殊的平行四边形,所以矩形的对边平行且相等.以上推理的方法是( )
| A.合情推理 | B.演绎推理 | C.归纳推理 | D.类比推理 |
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若 ,则 ,则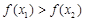 |
设a,b∈R,则“a+b=1”是“4ab≤1”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 的值是________.
的值是________.