题目内容
【题目】已知函数![]() .
.
(1)求曲线![]() 在点(
在点(![]() )处的切线方程;
)处的切线方程;
(2)证明:当![]() 时,
时,![]() 。
。
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)![]() ,由f′(0)=2,可得切线斜率k=2,即可得到切线方程;
,由f′(0)=2,可得切线斜率k=2,即可得到切线方程;
(2)可得![]() =﹣
=﹣![]() .可得f(x)在(﹣
.可得f(x)在(﹣![]() ),(2,+∞)递减,在(﹣
),(2,+∞)递减,在(﹣![]() ,2)递增,注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0,只需(x)
,2)递增,注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0,只需(x)![]() ≥﹣e,即可.
≥﹣e,即可.
(1)![]() =﹣
=﹣![]() .
.
∴f′(0)=2,即曲线y=f(x)在点(0,﹣1)处的切线斜率k=2,
∴曲线y=f(x)在点(0,﹣1)处的切线方程方程为y﹣(﹣1)=2x.
即2x﹣y﹣1=0为所求.
(2)证明:函数f(x)的定义域为:R,
可得![]() =﹣
=﹣![]() .
.
令f′(x)=0,可得![]() ,
,
当x![]() 时,f′(x)<0,x
时,f′(x)<0,x![]() 时,f′(x)>0,x∈(2,+∞)时,f′(x)<0.
时,f′(x)>0,x∈(2,+∞)时,f′(x)<0.
∴f(x)在(﹣![]() ),(2,+∞)递减,在(﹣
),(2,+∞)递减,在(﹣![]() ,2)递增,
,2)递增,
注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0
函数f(x)的图象如下:
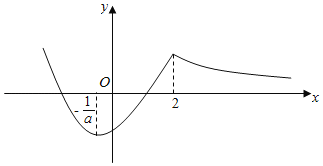
∵a≥1,∴![]() ,则
,则![]() ≥﹣e,
≥﹣e,
∴f(x)![]() ≥﹣e,
≥﹣e,
∴当a≥1时,f(x)+e≥0.

练习册系列答案
相关题目
【题目】以下资料是一位销售经理收集到的每年销售额y(千元)和销售经验x(年)的关系:
销售经验x/年 | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
年销售额y/千元 | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)依据这些数据画出散点图并作直线![]() =78+4.2x,计算
=78+4.2x,计算![]() ;
;
(2)依据这些数据求回归直线方程并据此计算![]() ;
;
(3)比较(1) (2)中的残差平方和![]() 的大小.
的大小.
