题目内容
【题目】如图,三棱柱![]() 的各棱长均相等,
的各棱长均相等, ![]() 底面
底面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)过![]() 作平面α,使得直线BE//平面α,若平面α与直线
作平面α,使得直线BE//平面α,若平面α与直线![]() 交于点H,指出点H所在的位置,并说明理由;
交于点H,指出点H所在的位置,并说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由直线![]() 平面
平面![]() ,利用线面平行的判定定理可得直线
,利用线面平行的判定定理可得直线![]() 直线
直线![]() ,又
,又![]() 直线
直线![]() ,可得四边形
,可得四边形![]() 是平行四边形,则
是平行四边形,则![]() ,即
,即![]() 点为
点为![]() 的中点;(2)取
的中点;(2)取![]() 的中点
的中点![]() ,由于
,由于![]() 两两互相垂直,所以可以
两两互相垂直,所以可以![]() 为轴建立如空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面
为轴建立如空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)如图所示,平面FHA1即为平面α,H点为线段BB1的中点.
理由如下:
因为直线BE//平面α,平面α∩平面AB1=A1H,直线BE平面AB1,
所以直线BE//直线A1H,又A1E//直线BH,
所以四边形BEA1H是平行四边形,则BH= A1E![]() ,
,
即H点为BB1的中点.
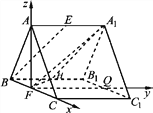
(2)如图,取B1C1的中点Q,显然FC,FQ,FA两两互相垂直,建立如图所示的空间直角坐标系F-xyz如图所示.
不妨设棱长为2,则H(-1,1,0),A1(0,2, ![]() ),
),
则![]() ,
, ![]() ,
,
设面FHA1的法向量![]() ,
,
则由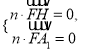 得
得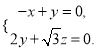
令![]() ,得
,得![]() .
.
取平面BFH的一个法向量![]() ,
,
于是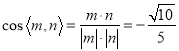 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面平行的证明以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】某超市计划销售某种食品,现邀甲、乙两个商家进场试销5天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利2元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利4元,超出30件的部分每件返利6元.经统计,两个商家的试销情况茎叶图如下:
甲 | 乙 | |||||||
9 | 8 | 9 | 2 | 8 | 8 | |||
2 | 2 | 3 | 2 | 1 | 1 | |||
(1)现从甲商家试销的5天中抽取两天,求这两天的销售量都小于30的概率;
(2)超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
【题目】在对人们的休闲方式的一次调查中,共调查了110人,其中女性50人,男性60人.女性中有30人主要的休闲方式是看电视,另外20人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外40人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断性别与休闲方式是否有关系.
下面临界值表供参考:
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式:K2=![]() )
)
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
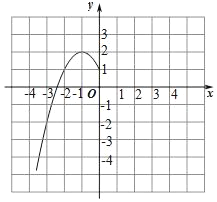
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.

(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.