题目内容
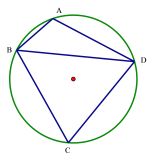
【题目】某城市在进行规划时,准备设计一个圆形的开放式公园.为达到社会和经济效益双丰收.园林公司进行如下设计,安排圆内接四边形![]() 作为绿化区域,其余作为市民活动区域.其中
作为绿化区域,其余作为市民活动区域.其中![]() 区域种植花木后出售,
区域种植花木后出售,![]() 区域种植草皮后出售,已知草皮每平方米售价为
区域种植草皮后出售,已知草皮每平方米售价为![]() 元,花木每平方米的售价是草皮每平方米售价的三倍. 若
元,花木每平方米的售价是草皮每平方米售价的三倍. 若![]() km ,
km ,![]() km
km
(1)若![]() km ,求绿化区域的面积;
km ,求绿化区域的面积;
(2)设![]() ,当
,当![]() 取何值时,园林公司的总销售金额最大.
取何值时,园林公司的总销售金额最大.
【答案】(1)绿化区域的面积为![]()
![]() ;(2)当
;(2)当![]() 时,园林公司的销售金额最大,最大为
时,园林公司的销售金额最大,最大为![]() 百万元.
百万元.
【解析】
(1)若![]() km,可得
km,可得![]() ,进而求出
,进而求出![]() ,即可求绿化区域的面积(2)设
,即可求绿化区域的面积(2)设![]() ,求出园林公司的总销售金额,利用导数可得结论.
,求出园林公司的总销售金额,利用导数可得结论.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得,![]()
因为![]() , 所以
, 所以![]() ,
,
又因为![]() 、
、![]() 、
、![]() 、
、![]() 共圆,所以
共圆,所以![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
将![]() ,
,![]() 代入化简得
代入化简得![]() ,
,
解得![]() (
(![]() 舍去).
舍去).
所以![]()
即绿化空间的面积为![]()
![]()
(2)在![]() 、
、![]() 中分别利用余弦定理得
中分别利用余弦定理得
![]() ①
①
![]() ②
②
联立①②消去![]() 得
得![]() ,得
,得
![]() ,解得
,解得![]() (
(![]() 舍去).
舍去).
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
![]()
![]()
因为草皮每平方米售价为![]() 元,则花木每平方米售价为
元,则花木每平方米售价为![]() 元,设销售金额为
元,设销售金额为![]() 百万元.
百万元.
![]()
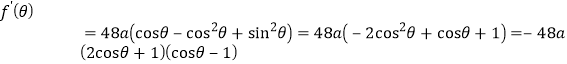
令![]() ,解得
,解得![]() ,又
,又![]() ,妨设
,妨设![]() ,
,
则函数![]() 在
在![]() 上为增函数;
上为增函数;
令![]() ,解得
,解得![]() ,则函数
,则函数![]() 在
在![]() 上为减函数,
上为减函数,
所以当![]() 时,
时,![]() .
.
答:(1)绿化区域的面积为![]()
![]() ;(2)当
;(2)当![]() 时,园林公司的销售金额最大,最大为
时,园林公司的销售金额最大,最大为![]() 百万元.
百万元.

练习册系列答案
相关题目