题目内容
【题目】如图,点![]() 在抛物线
在抛物线![]() 外,过点
外,过点![]() 作抛物线
作抛物线![]() 的两切线,设两切点分别为
的两切线,设两切点分别为![]() ,
,![]() ,记线段
,记线段![]() 的中点为
的中点为![]() .
.

(Ⅰ)求切线![]() ,
,![]() 的方程;
的方程;
(Ⅱ)证明:线段![]() 的中点
的中点![]() 在抛物线
在抛物线![]() 上;
上;
(Ⅲ)设点![]() 为圆
为圆![]() 上的点,当
上的点,当![]() 取最大值时,求点
取最大值时,求点![]() 的纵坐标.
的纵坐标.
【答案】(Ⅰ)切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() .
.
(Ⅱ)见证明;(Ⅲ)![]()
【解析】
(Ⅰ)结合导数的几何意义可得切线![]() ,
,![]() 的方程;(Ⅱ)由(1)可得
的方程;(Ⅱ)由(1)可得![]() ,
,![]() ,故
,故![]() ,
,![]() .再结合M点的坐标即可明确
.再结合M点的坐标即可明确![]() 在抛物线
在抛物线![]() 上;(Ⅲ)由题意可得
上;(Ⅲ)由题意可得![]() . 设
. 设![]() ,则
,则![]() .结合均值不等式即可得到结果.
.结合均值不等式即可得到结果.
(Ⅰ)切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
同理可得,切线![]() 的方程为
的方程为![]() .
.
(另解:设切线![]() 的方程为:
的方程为:![]()
由 消去
消去![]() 后可得:
后可得:![]()
![]() ∴
∴![]()
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
同理可得,切线![]() 的方程为
的方程为![]() .
.

(Ⅱ)因为点![]() 既在切线
既在切线![]() 上,也在切线
上,也在切线![]() 上,
上,
由(1)可得![]() ,
,![]() ,故
,故![]() ,
,![]() .
.
又点![]() 的坐标为
的坐标为![]() .
.
所以点![]() 的纵坐标为
的纵坐标为![]() ,
,
即点![]() 的坐标为
的坐标为![]() .故
.故![]() 在抛物线
在抛物线![]() 上.
上.
(Ⅲ)由(Ⅰ)知:![]()
![]() ,
,
![]() ,所以
,所以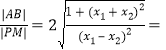
![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,即当
时,即当![]() 时,
时,![]() 取最大值.
取最大值.

 培优三好生系列答案
培优三好生系列答案【题目】某蛋糕店制作并销售一款蛋糕,当天每售出![]() 个获得利润
个获得利润![]() 元,未售出的每个亏损
元,未售出的每个亏损![]() 元.根据以往
元.根据以往![]() 天的资料统计,得到如下需求量表.元日这天,此蛋糕店制作了这款蛋糕
天的资料统计,得到如下需求量表.元日这天,此蛋糕店制作了这款蛋糕![]() 个.以
个.以![]() (单位:个,
(单位:个, ![]() )表示这天的市场需求量.
)表示这天的市场需求量. ![]() (单位:元)表示这天出售这款蛋糕获得的利润.
(单位:元)表示这天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
, ![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于
不少于![]() 元的天数中,按需求量分层抽样抽取
元的天数中,按需求量分层抽样抽取![]() 天,
天,
(ⅰ)求这![]() 天中利润为
天中利润为![]() 元的天数;
元的天数;
(ⅱ)再从这![]() 天中抽取
天中抽取![]() 天做进一步分析,设这
天做进一步分析,设这![]() 天中利润为
天中利润为![]() 元的天数为
元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某地区对一种新品种小麦在一块试验田进行试种.从试验田中抽取![]() 株小麦,测量这些小麦的生长指标值,由测量结果得如下频数分布表:
株小麦,测量这些小麦的生长指标值,由测量结果得如下频数分布表:
生长指标值分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)求这![]() 株小麦生长指标值的样本平均数
株小麦生长指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)由直方图可以认为,这种小麦的生长指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() .
.
①利用该正态分布,求![]() ;
;
②若从试验田中抽取![]() 株小麦,记
株小麦,记![]() 表示这
表示这![]() 株小麦中生长指标值位于区间
株小麦中生长指标值位于区间![]() 的小麦株数,利用①的结果,求
的小麦株数,利用①的结果,求![]() .
.
附: ![]() .
.
若![]() ,则
,则![]() ,
,
![]() .
.


