题目内容
【题目】已知椭圆![]() 两焦点
两焦点![]() ,并经过点
,并经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 上关于
上关于![]() 轴对称的不同两点,
轴对称的不同两点,![]() 为
为![]() 轴上两点,且
轴上两点,且![]() ,证明:直线
,证明:直线![]() 的交点
的交点![]() 仍在椭圆
仍在椭圆![]() 上;
上;
(3)你能否将(2)推广到一般椭圆中?写出你的结论即可.
【答案】(1)![]() ;(2)证明见解析;(3)若椭圆
;(2)证明见解析;(3)若椭圆![]() ,若
,若![]() ,则直线
,则直线![]() 的交点
的交点![]() 仍在椭圆
仍在椭圆![]() 上;
上;
【解析】
(1)已知焦点![]() ,利用椭圆的定义,求得椭圆的长轴长,再求得
,利用椭圆的定义,求得椭圆的长轴长,再求得![]() ,写出方程即可.
,写出方程即可.
(2)设![]() ,得到直线
,得到直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,设设交点
,设设交点![]() ,分别代入直线
,分别代入直线![]() ,
,![]() 的方程得
的方程得![]() ,
,![]() ,两式化简得到
,两式化简得到![]() ,说明交点在椭圆上.
,说明交点在椭圆上.
(3)根据(2)的论证过程,推知规律是![]() .
.
根据题意,椭圆的长轴长: ,
,
解得![]() ,
,
又![]() ,
,
所以椭圆的方程是![]() .
.
(2)设![]() ,
,
则直线![]() 的方程为
的方程为![]() ①,
①,
直线![]() 的方程为
的方程为![]() ②
②
设交点![]() ,代入①②得
,代入①②得
![]() ③ ,
③ ,
![]() ④,
④,
③与④两边分别相乘得
![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() ,
,
所以直线![]() 的交点
的交点![]() 的坐标适合椭圆的方程,
的坐标适合椭圆的方程,
所以直线![]() 的交点
的交点![]() 仍在椭圆
仍在椭圆![]() 上.
上.
(3)若椭圆![]() ,若
,若![]() ,则直线
,则直线![]() 的交点
的交点![]() 仍在椭圆
仍在椭圆![]() 上;
上;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂每年定期对职工进行培训以提高工人的生产能力(生产能力是指一天加工的零件数).现有![]() 、
、![]() 两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
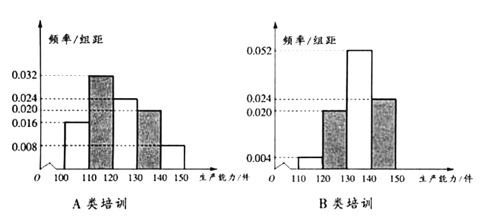
(1)记![]() 表示事件“参加
表示事件“参加![]() 类培训工人的生产能力不低于130件”,估计事件
类培训工人的生产能力不低于130件”,估计事件![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为工人的生产能力与培训类有关:
的把握认为工人的生产能力与培训类有关:
生产能力 | 生产能力 | 总计 | |
| 50 | ||
| 50 | ||
总计 | 100 |
(3)根据频率分布直方图,判断哪类培训更有利于提高工人的生产能力,请说明理由.
参考数据
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.