题目内容
(本题满分12分)
已知函数 (
( 为非零常数,
为非零常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(1)判断 的单调性;
的单调性;
(2)若 , 求
, 求 的最大值.
的最大值.
(Ⅰ)在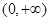 上是减函数.(Ⅱ)当
上是减函数.(Ⅱ)当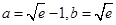 时,
时,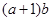 的最大值为
的最大值为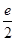 。
。
解析

练习册系列答案
相关题目
题目内容
(本题满分12分)
已知函数 (
( 为非零常数,
为非零常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(1)判断 的单调性;
的单调性;
(2)若 , 求
, 求 的最大值.
的最大值.
(Ⅰ)在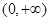 上是减函数.(Ⅱ)当
上是减函数.(Ⅱ)当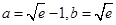 时,
时,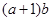 的最大值为
的最大值为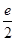 。
。
解析
