题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列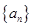 的前
的前 项和为
项和为 ,点列
,点列 在函数
在函数 的图象上。
的图象上。
(1)求函数 的解析式;
的解析式;
(2)若 ,求
,求 的值;
的值;
(3)令 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.
第3小题满分6分.
设
 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列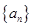 的前
的前 项和为
项和为 ,点列
,点列 在函数
在函数 的图象上。
的图象上。(1)求函数
 的解析式;
的解析式;(2)若
 ,求
,求 的值;
的值;(3)令
 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.解:(1)由条件可知, ……………2分
……………2分
因为关于 的不等式
的不等式 的解集为
的解集为 ,所以
,所以 ……………3分
……………3分
即函数 的解析式为
的解析式为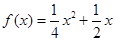 ……………4分
……………4分
(2)因为点列 在函数
在函数 的图象上,所以
的图象上,所以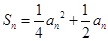
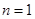 代入,
代入, ,即
,即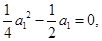 因为
因为 ,所以
,所以 ;……………6分
;……………6分
当 时,
时,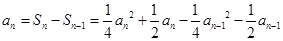 ,
,
化简得: ……………7分
……………7分
因为 所以
所以 ,即数列
,即数列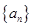 为等差数列,且
为等差数列,且 。……………9分
。……………9分
则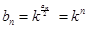 ,所以
,所以 。……………12分
。……………12分
(3)在数列 的前
的前 项中
项中
 为奇数时,
为奇数时, ,所以
,所以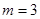 ……………14分
……………14分
 为偶数时,要满足
为偶数时,要满足 ,则
,则 ……………16分
……………16分
所以,满足 的所有项数之和为
的所有项数之和为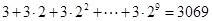 ……………18分
……………18分
 ……………2分
……………2分因为关于
 的不等式
的不等式 的解集为
的解集为 ,所以
,所以 ……………3分
……………3分即函数
 的解析式为
的解析式为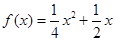 ……………4分
……………4分(2)因为点列
 在函数
在函数 的图象上,所以
的图象上,所以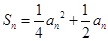
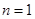 代入,
代入, ,即
,即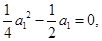 因为
因为 ,所以
,所以 ;……………6分
;……………6分当
 时,
时,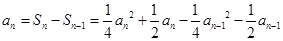 ,
,化简得:
 ……………7分
……………7分因为
 所以
所以 ,即数列
,即数列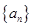 为等差数列,且
为等差数列,且 。……………9分
。……………9分则
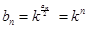 ,所以
,所以 。……………12分
。……………12分(3)在数列
 的前
的前 项中
项中 为奇数时,
为奇数时, ,所以
,所以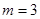 ……………14分
……………14分 为偶数时,要满足
为偶数时,要满足 ,则
,则 ……………16分
……………16分所以,满足
 的所有项数之和为
的所有项数之和为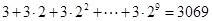 ……………18分
……………18分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
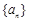 中,公比
中,公比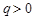 ,数列的前n项和为
,数列的前n项和为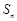 ,若
,若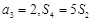 ,求数列
,求数列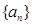 的前n项和为
的前n项和为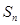 ,且
,且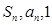 成等差数列.
成等差数列. 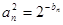 ,设
,设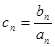 求数列
求数列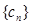 的前项和
的前项和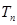 .
.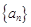 是首项
是首项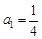 的等比数列,其前
的等比数列,其前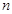 项和
项和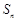 中
中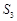 ,
,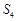 ,
,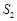 成等差数列,
成等差数列,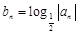 ,若
,若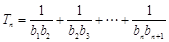 ,求证:
,求证: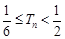 .
.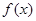 是定义在
是定义在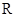 上恒不为0的函数,对任意
上恒不为0的函数,对任意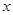 、
、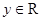 都有
都有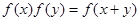 ,若
,若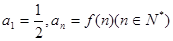 ,则数列
,则数列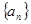 的前n项和
的前n项和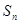 为
为 



 }中,已知
}中,已知 ,
, ,则
,则




 中,已知对任意
中,已知对任意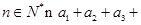 …
… 则
则 …
… 等于
等于



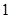 ,各项的和
,各项的和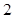 ,则 公比q=_______________
,则 公比q=_______________