题目内容
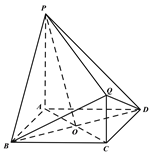
【题目】如图, ![]() 都与正方形
都与正方形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]()
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)过点![]() 与平面
与平面![]() 平行的平面交
平行的平面交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由条件得三角形PAD为等腰三角形,再根据等腰三角形性质得![]() .计算由勾股定理得
.计算由勾股定理得![]() ,最后根据线面垂直判定定理得
,最后根据线面垂直判定定理得![]() ⊥平面
⊥平面![]() ;(2)设点
;(2)设点![]() 与平面
与平面![]() 平行的平面交
平行的平面交![]() 于点
于点![]() ,由面面平行性质定理得
,由面面平行性质定理得![]() ,所以
,所以![]()
试题解析:(Ⅰ)连接![]() ,由题知
,由题知![]() ,
,
![]() 共面,
共面, ![]() ,
,
∴![]() ,
,
![]()
∴![]() .
.
由题中数据得
![]()
![]()
![]() ∴
∴![]() ∽
∽![]() ∴
∴![]() ,
,
又∵![]()
∴![]()
∴![]()
(或计算![]() ,由勾股定理得出
,由勾股定理得出![]() )
)
∵![]() ,
,
∴![]()
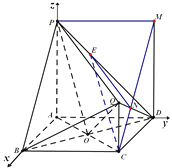
(Ⅱ)如图,以![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴建立直角坐标系,
轴建立直角坐标系,
∴各点坐标分别为![]() ,
,
∴![]() =
=![]() ,
, ![]() =
=![]() ,设平面
,设平面![]() 的法向量
的法向量![]()
∴![]() ,得
,得![]() ,
,
不妨设![]() ,∴
,∴![]()
设![]() ,∴
,∴![]() ,
,![]()
![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 与平面
与平面![]() 的法向量
的法向量![]() 垂直。
垂直。
![]() ,
,
∴![]() . ∴
. ∴![]()
(方法二)在平面![]() 中,分别过
中,分别过![]() 点、
点、![]() 点作直线
点作直线![]() 的平行线相交于点
的平行线相交于点![]() ,
,
连结![]() 交直线
交直线![]() 与点
与点![]() ,在平面
,在平面![]() 中过点
中过点![]()
作直线![]() 交
交![]() 于点
于点![]() ,
,
由题可知![]()
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ∵
∵![]() , ∴
, ∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目