题目内容
10.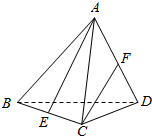 如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.
如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.求:(1)CF与平面BCD所成的正弦角.
(2)AE与CF所成的角的余弦值.
分析 (1)根据ABCD为正四面体,可设底面BCD的中心为O,连接DE,并过O作MN∥BC,从而可以看出ON,OD,OA三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,然后可确定图形上一些点的坐标,从而求出向量$\overrightarrow{CF},\overrightarrow{OA},\overrightarrow{AE}$的坐标.可以看出$\overrightarrow{OA}$为平面BCD的一条法向量,设CF和平面BCD所成角为θ,根据sinθ=$|cos<\overrightarrow{CF},\overrightarrow{OA}>|$即可求出sinθ;
(2)根据$cos<\overrightarrow{AE},\overrightarrow{CF}>=\frac{\overrightarrow{AE}•\overrightarrow{CF}}{|\overrightarrow{AE}||\overrightarrow{CF}|}$即可求出向量$\overrightarrow{AE},\overrightarrow{CF}$所夹角的余弦值,从而对求得的余弦值取绝对值便可得出AE与CF所成角的余弦值.
解答 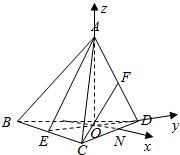 解:设底面BCD的中心为O,连接DE,则O在DE上,过O作MN∥BC,分别交BD,CD于M,N,则:
解:设底面BCD的中心为O,连接DE,则O在DE上,过O作MN∥BC,分别交BD,CD于M,N,则:
ON,OD,OA三直线两两垂直,分别以这三直线为x,y,z轴建立如图所示空间直角坐标系,设该正四面体的棱长为1,则:
O(0,0,0),D(0,$\frac{\sqrt{3}}{3}$,0),A(0,0,$\frac{\sqrt{6}}{3}$),F(0,$\frac{\sqrt{3}}{6}$,$\frac{\sqrt{6}}{6}$),C($\frac{1}{2},-\frac{\sqrt{3}}{6},0$),E(0,$-\frac{\sqrt{3}}{6}$,0);
∴$\overrightarrow{CF}=(-\frac{1}{2},\frac{\sqrt{3}}{3},\frac{\sqrt{6}}{6})$,$\overrightarrow{OA}=(0,0,\frac{\sqrt{6}}{3})$,$\overrightarrow{AE}=(0,-\frac{\sqrt{3}}{6},-\frac{\sqrt{6}}{3})$;
∴(1)$\overrightarrow{OA}$是平面BCD的法向量,设直线CF和平面BCD所成角为θ,则:
sinθ=$|cos<\overrightarrow{CF},\overrightarrow{OA}>|$=$\frac{|\overrightarrow{CF}•\overrightarrow{OA}|}{|\overrightarrow{CF}||\overrightarrow{OA}|}=\frac{\frac{1}{3}}{\sqrt{\frac{1}{4}+\frac{1}{3}+\frac{1}{6}}•\frac{\sqrt{6}}{3}}$=$\frac{\sqrt{2}}{3}$;
∴CF与平面BCD所成角的正弦值为$\frac{\sqrt{2}}{3}$;
(2)$cos<\overrightarrow{AE},\overrightarrow{CF}>=\frac{\overrightarrow{AE}•\overrightarrow{CF}}{|\overrightarrow{AE}||\overrightarrow{CF}|}$=$\frac{-\frac{1}{6}-\frac{1}{3}}{\sqrt{\frac{1}{12}+\frac{2}{3}}•\sqrt{\frac{1}{4}+\frac{1}{3}+\frac{1}{6}}}$=$-\frac{2}{3}$;
∴AE与CF所成的角的余弦值为$\frac{2}{3}$.
点评 考查正四面体的概念,三角形重心的性质,正三角形中心的概念,以及通过建立空间直角坐标系,利用空间向量解决线面角及线线角的问题的方法,能求空间点的坐标,根据点的坐标可求向量坐标,平面法向量的概念,向量夹角余弦的坐标公式,清楚向量夹角和线面角及异面直线所成角的关系.

| A. | x1y1+x2y2 | B. | x1x2+y1y2 | C. | x1y2+x2y1 | D. | $\frac{1}{2}$ |
