题目内容
5.在平面四边形ABCD中,向量$\overrightarrow{a}$=$\overrightarrow{AB}$=(4,1),$\overrightarrow{b}$=$\overrightarrow{BC}$=(3,1),$\overrightarrow{c}$=$\overrightarrow{CD}$=(-1,-2)(!)若向量($\overrightarrow{a}$+2$\overrightarrow{b}$)与向量($\overrightarrow{b}$-k$\overrightarrow{c}$)垂直,求实数k的值;
(2)若$\overrightarrow{DB}$=m$\overrightarrow{DA}$+n$\overrightarrow{DC}$,求实数m,n.
分析 (1)利用向量垂直与数量积的关系即可得出;
(2)利用向量的坐标运算、向量相等即可得出.
解答 解:(1)$\overrightarrow{a}$+2$\overrightarrow{b}$=(10,3),$\overrightarrow{b}$-k$\overrightarrow{c}$=(3+k,1+2k),
∵向量($\overrightarrow{a}$+2$\overrightarrow{b}$)与向量($\overrightarrow{b}$-k$\overrightarrow{c}$)垂直,
∴($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{b}$-k$\overrightarrow{c}$)=10(3+k)+3(1+2k)=0,
解得k=-$\frac{33}{16}$.
(2)$\overrightarrow{DB}$=$\overrightarrow{DC}+\overrightarrow{CB}$=(1,2)-(3,1)=(-2,1).
$\overrightarrow{DA}$=$\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}$=(1,2)+(-3,-1)+(-4,-1)=(-6,0).
若$\overrightarrow{DB}$=m$\overrightarrow{DA}$+n$\overrightarrow{DC}$,
∴(-2,1)=m(-6,0)+n(1,2),
∴$\left\{\begin{array}{l}{-2=-m+n}\\{1=2n}\end{array}\right.$,
解得m=$\frac{5}{2}$,n=$\frac{1}{2}$.
点评 本题考查了向量垂直与数量积的关系、向量的坐标运算、向量相等,考查了推理能力与计算能力,属于中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | x-2y+1=0 | B. | 2x-y-1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,M是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,M是PC的中点.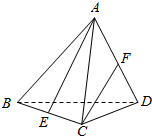 如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.
如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.