��Ŀ����
2����֪����g��x��=$\frac{1}{cos��•x}$+lnx��[1��+�ޣ���Ϊ����������$�ȡ�[0��\frac{��}{2}��$��f��x��=mx-$\frac{m-1}{x}$-lnx��m��R����1����ȵ�ȡֵ��Χ��
��2����h��x��=f��x��-g��x����[1��+�ޣ���Ϊ������������m��ȡֵ��Χ��
��3������[1��e]�����ٴ���һ��x0��ʹ��h��x0����$\frac{2e}{x_0}$��������m��ȡֵ��Χ��
���� ��1������$g'��x��=-\frac{1}{{cos��•{x^2}}}+\frac{1}{x}��0$��[1��+�ޣ��Ϻ�������Ƴ�cos�ȡ�1�����ɵõ��ȵ�ȡֵ��Χ��
��2�����$h��x��=mx-\frac{m}{x}-2lnx$��ͨ��h��x����[1���ޣ���Ϊ�����������Ƴ�������mx2-2x+m��0����mx2-2x+m��0��[1���ޣ���������õ�$m��\frac{2x}{{1+{x^2}}}$��ͨ����������ʽ���m��ȡֵ��Χ��
��3�����캯��$F��x��=mx-\frac{m}{x}-2lnx-\frac{2e}{x}$��
��m��0ʱ����m��0ʱ���ֱ�ͨ��F'��x����0��[1��e]����������m��ȡֵ��Χ��
��� ��12�֣��⣺��1�������⣬$g'��x��=-\frac{1}{{cos��•{x^2}}}+\frac{1}{x}��0$��[1��+�ޣ��Ϻ��������$\frac{cos��•x-1}{{cos��•{x^2}}}��0$��$�ȡ�[0��\frac{��}{2}��$����cos��•x-1��0��[1��+�ޣ��Ϻ������
ֻ��cos��•1-1��0����cos�ȡ�1���æ�=0���ʦȵ�ȡֵ��Χ��{0}
��2���ɣ�1������$h��x��=mx-\frac{m}{x}-2lnx$����${h^��}��x��=\frac{{m{x^2}-2x+m}}{x^2}$��
��h��x����[1���ޣ���Ϊ������������mx2-2x+m��0����mx2-2x+m��0��[1���ޣ��������
mx2-2x+m��0�ȼ���m��1+x2����2x����$m��\frac{2x}{{1+{x^2}}}$��
��$\frac{2x}{{1+{x^2}}}=\frac{2}{{x+\frac{1}{x}}}��\left\{{\frac{2}{{x+\frac{1}{x}}}}\right\}max=1��m��1$��
��mx2-2x+m��0�ȼ���m��1+x2����2x��
��$m��\frac{2x}{{1+{x^2}}}$��[1���ޣ��������
��$\frac{2x}{{1+{x^2}}}�ʣ�{0��1}]$����m��0��
���ϣ�m��ȡֵ��Χ�ǣ�-�ޣ�0]��[1��+�ޣ���
��3�����캯��$F��x��=mx-\frac{m}{x}-2lnx-\frac{2e}{x}$��
��m��0ʱ��$x��[{1��e}]��mx-\frac{m}{x}��0$��$-2lnx-\frac{2e}{x}��0$��������[1��e]�ϲ�����һ��x0��
ʹ��$h��{x_0}����\frac{2e}{x_0}$������
��m��0ʱ��$F'��x��=m+\frac{m}{x^2}-\frac{2}{x}+\frac{2e}{x^2}=\frac{{m{x^2}-2x+m+2e}}{x^2}$��
��Ϊx��[1��e]������2e-2x��0��mx2+m��0������F�䣨x����0��[1��e]�������
��F��x����[1��e]�ϵ���������$F{��x��_{max}}=me-\frac{4}{e}-4$��ֻҪ$me-\frac{4}{e}-4��0$��
���$m��\frac{4e}{{{e^2}-1}}$��
��m��ȡֵ��Χ��$��{\frac{4e}{{{e^2}-1}}��+��}��$��
���� ���⿼�麯���Ķ������ۺ�Ӧ�ã���������ֵ�Լ������ĵ����Ե�Ӧ�ã�������������������������ת��˼���Ӧ�ã�

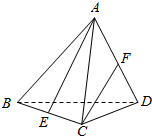 ��ͼ��ʾ��ABCD��һ���������壬E��F�ֱ�ΪBC��AD���е㣮
��ͼ��ʾ��ABCD��һ���������壬E��F�ֱ�ΪBC��AD���е㣮��1��CF��ƽ��BCD���ɵ����ҽǣ�
��2��AE��CF���ɵĽǵ�����ֵ��
| A�� | x-2y+1=0 | B�� | 2x-y-1=0 | C�� | x-y+3=0 | D�� | x-y-3=0 |
| A�� | ��a-1��f��1��+��2-a��f��2�� | B�� | ��2-a��f��1��+��a-1��f��2�� | C�� | ��2-a��f��1��+��1-a��f��2�� | D�� | ��1-a��f��1��+��2-a��f��2�� |
| A�� | [-4��2] | B�� | [-4��-1���ȣ�-1��2] | C�� | ��-4��2�� | D�� | ��-4��-1���ȣ�-1��2�� |