题目内容
(本小题满分12分)已知函数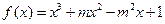 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为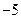 的直线是曲线
的直线是曲线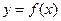 的切线,求此直线方程.
的切线,求此直线方程.
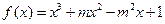 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.(Ⅰ)求m的值;
(Ⅱ)若斜率为
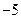 的直线是曲线
的直线是曲线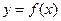 的切线,求此直线方程.
的切线,求此直线方程.m=2.,5x+y-1=0,或135x+27y-23=0
解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=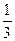 m. …………2分
m. …………2分
当x变化时,f’(x)与f(x)的变化情况如下表:
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1="9, " …………6分
∴m=2. …………7分
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1, 依题意知f’(x)=3x2+4x-4=-5,
∴x=-1或x=-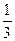 . …………9分
. …………9分
又f(-1)=6,f(-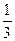 )=
)=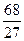 , …………10分
, …………10分
所以切线方程为y-6=-5(x+1),或y-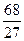 =-5(x+
=-5(x+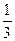 ),
),
即所求的直线方程为: 5x+y-1=0,或135x+27y-23=0 . …………12分
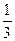 m. …………2分
m. …………2分当x变化时,f’(x)与f(x)的变化情况如下表:
| x | (-∞,-m) | -m | (-m,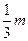 ) ) | 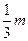 | (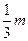 ,+∞) ,+∞) |
| f’(x) |  + + | 0 | - | 0 | + |
| f (x) | | 极大值 | | 极小值 | |
即f(-m)=-m3+m3+m3+1="9, " …………6分
∴m=2. …………7分
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1, 依题意知f’(x)=3x2+4x-4=-5,
∴x=-1或x=-
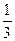 . …………9分
. …………9分又f(-1)=6,f(-
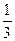 )=
)=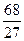 , …………10分
, …………10分所以切线方程为y-6=-5(x+1),或y-
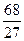 =-5(x+
=-5(x+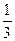 ),
),即所求的直线方程为: 5x+y-1=0,或135x+27y-23=0 . …………12分

练习册系列答案
相关题目
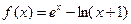 。
。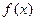 的最小值; (Ⅱ)已知
的最小值; (Ⅱ)已知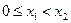 ,求证:
,求证: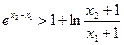 。
。 (
(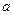 为常数)在点
为常数)在点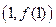 处
处 的斜率为
的斜率为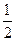 .
.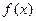 在区间
在区间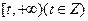 上存在极值,求
上存在极值,求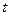 的最大值;
的最大值;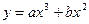 ,当
,当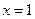 时,有极大值
时,有极大值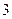 .
.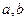 的值; (2)求函数
的值; (2)求函数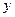 的极小值。
的极小值。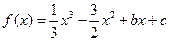 ,且
,且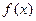 在
在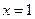 处取得极值.
处取得极值.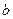 的值;
的值;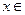 [-1,
[-1,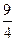 ]时,
]时,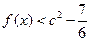 恒成立,求
恒成立,求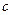 的取值范围.
的取值范围.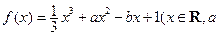 ,
,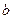 为实数)有极值,且在
为实数)有极值,且在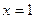 处的切线与直线
处的切线与直线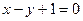 平行.
平行.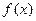 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;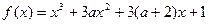 有极大值又有极小值,则
有极大值又有极小值,则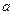 的取值范围是 .
的取值范围是 .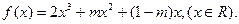
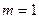 时,解不等式
时,解不等式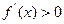 ;
;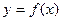 的所有切线中,切线斜率的最小值为
的所有切线中,切线斜率的最小值为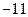 ,求
,求 的值.
的值.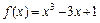 在区间[
在区间[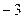 ,0]上的最小值是
,0]上的最小值是