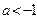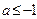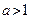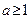题目内容
已知函数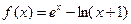 。
。
(I)求函数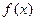 的最小值; (Ⅱ)已知
的最小值; (Ⅱ)已知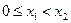 ,求证:
,求证: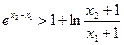 。
。
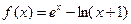 。
。(I)求函数
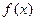 的最小值; (Ⅱ)已知
的最小值; (Ⅱ)已知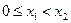 ,求证:
,求证: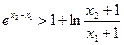 。
。(1)1(2)见解析
(Ⅰ)函数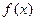 的定义域是
的定义域是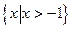 ,
,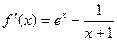 …………2分
…………2分
当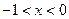 时,∵
时,∵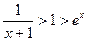 ∴
∴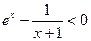 即
即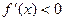
这说明函数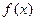 在区间
在区间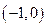 上是减函数 ……………4分
上是减函数 ……………4分
当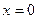 时,
时,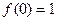 …………5分
…………5分
当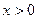 时, ∵
时, ∵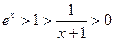 ∴
∴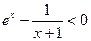 即
即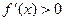
这说明函数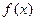 在区间
在区间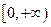 上是增函数 ………………6分
上是增函数 ………………6分
故当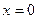 时,
时,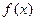 取得最小值
取得最小值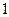 ……7分
……7分
(Ⅱ)由(1)知,当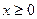 时,
时,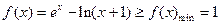 ……8分
……8分
而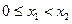 ,
,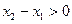 ,因此
,因此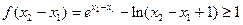
∴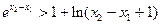 ① …12分
① …12分
又
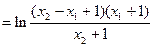
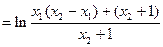
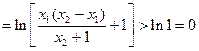
∴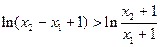 ② …13分
② …13分
综合①、②得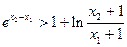 成立 …14分
成立 …14分
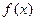 的定义域是
的定义域是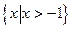 ,
,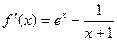 …………2分
…………2分当
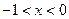 时,∵
时,∵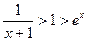 ∴
∴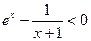 即
即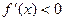
这说明函数
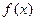 在区间
在区间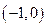 上是减函数 ……………4分
上是减函数 ……………4分当
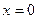 时,
时,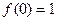 …………5分
…………5分当
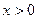 时, ∵
时, ∵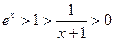 ∴
∴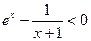 即
即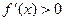
这说明函数
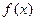 在区间
在区间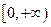 上是增函数 ………………6分
上是增函数 ………………6分故当
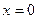 时,
时,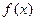 取得最小值
取得最小值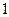 ……7分
……7分(Ⅱ)由(1)知,当
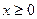 时,
时,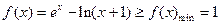 ……8分
……8分而
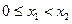 ,
,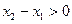 ,因此
,因此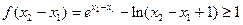
∴
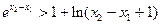 ① …12分
① …12分又

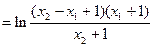
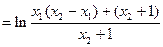
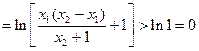
∴
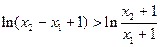 ② …13分
② …13分综合①、②得
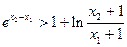 成立 …14分
成立 …14分
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
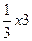 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。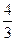 ,试确定b、c的值;
,试确定b、c的值;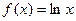
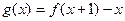 的最大值;
的最大值; 时,求证
时,求证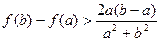 ;
;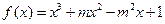 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.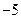 的直线是曲线
的直线是曲线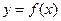 的切线,求此直线方程.
的切线,求此直线方程.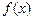 的导数
的导数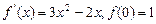 .求函数
.求函数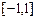 上的最小值与最大值.
上的最小值与最大值.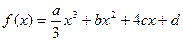 的图象关于原点对称,
的图象关于原点对称,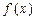 的图象在点
的图象在点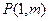 处的切线的斜率为
处的切线的斜率为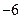 ,且当
,且当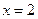 时
时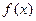 有极值.
有极值.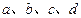 的值;
的值; 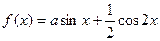 (
(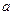 为常数)在
为常数)在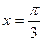 处取得极值,则
处取得极值,则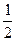
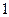
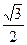
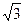
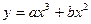 ,当
,当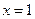 时,有极大值
时,有极大值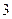 ;
;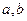 的值;(2)求函数
的值;(2)求函数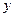 的极小值。
的极小值。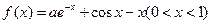 若对任意的
若对任意的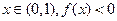 恒成立,则
恒成立,则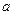 的取值范围( )
的取值范围( )