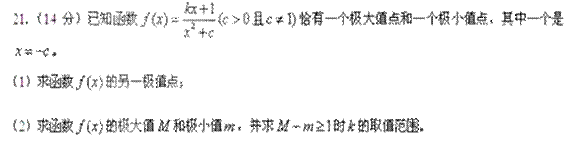题目内容
已知函数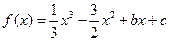 ,且
,且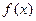 在
在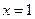 处取得极值.
处取得极值.
(1)求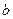 的值;
的值;
(2)若当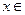 [-1,
[-1,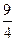 ]时,
]时,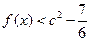 恒成立,求
恒成立,求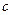 的取值范围.
的取值范围.
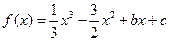 ,且
,且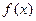 在
在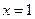 处取得极值.
处取得极值.(1)求
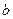 的值;
的值;(2)若当
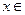 [-1,
[-1,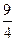 ]时,
]时,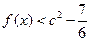 恒成立,求
恒成立,求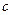 的取值范围.
的取值范围.(1)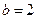
(2)(-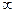 ,-1)
,-1)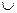 (2,+
(2,+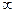 )
)
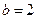
(2)(-
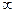 ,-1)
,-1)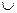 (2,+
(2,+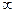 )
)(1)因为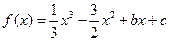 ,
,
所以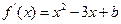 .……………………………………………2分
.……………………………………………2分
因为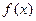 在
在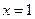 处取得极值,
处取得极值,
所以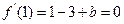 .…………………………………………4分
.…………………………………………4分
解得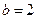 .……………………………………………………5分
.……………………………………………………5分
(2)因为 .
.
所以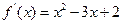
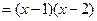 ,……………………………………………………6分
,……………………………………………………6分
当 变化时,
变化时,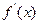 ,
,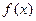 的变化情况如下表:
的变化情况如下表:
因此当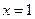 时,
时,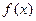 有极大值
有极大值 .…………………………………8分
.…………………………………8分
又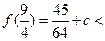
 ,
,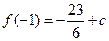

 ,
,
∴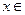 [-1,
[-1, 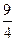 ]时,
]时,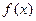 最大值为
最大值为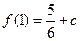 .………………10分
.………………10分
∴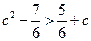 . ……………………………………………………12分
. ……………………………………………………12分
∴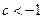 或
或 .
.
∴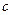 的取值范围为(-
的取值范围为(-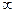 ,-1)
,-1)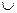 (2,+
(2,+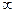 )……………………………14分
)……………………………14分
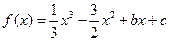 ,
,所以
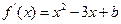 .……………………………………………2分
.……………………………………………2分因为
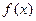 在
在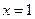 处取得极值,
处取得极值,所以
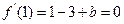 .…………………………………………4分
.…………………………………………4分解得
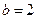 .……………………………………………………5分
.……………………………………………………5分(2)因为
 .
.所以
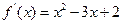
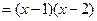 ,……………………………………………………6分
,……………………………………………………6分当
 变化时,
变化时,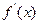 ,
,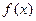 的变化情况如下表:
的变化情况如下表: | -1 | 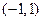 | 1 | 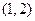 | 2 | 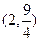 | 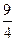 |
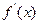 | | 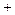 | 0 | 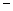 | 0 | 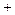 | |
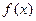 | 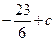 | 单调递增 |  |  单调递减 单调递减 | 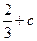 | 单调递增 | 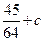 |
因此当
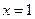 时,
时,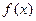 有极大值
有极大值 .…………………………………8分
.…………………………………8分又
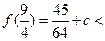
 ,
,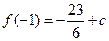

 ,
,∴
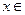 [-1,
[-1, 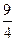 ]时,
]时,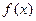 最大值为
最大值为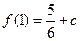 .………………10分
.………………10分∴
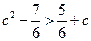 . ……………………………………………………12分
. ……………………………………………………12分∴
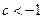 或
或 .
.∴
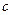 的取值范围为(-
的取值范围为(-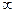 ,-1)
,-1) (2,+
(2,+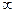 )……………………………14分
)……………………………14分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
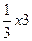 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。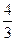 ,试确定b、c的值;
,试确定b、c的值;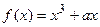 与
与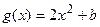 的图象有公共点
的图象有公共点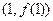 ,且它们的图象在该点处的切线相同。记
,且它们的图象在该点处的切线相同。记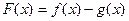 。
。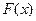 的表达式,并求
的表达式,并求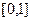 上的值域;
上的值域;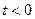 ,函数
,函数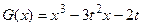 ,
,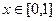 。若对于任意
。若对于任意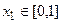 ,总存在
,总存在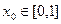 ,使得
,使得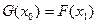 ,求实数
,求实数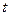 的取值范围。
的取值范围。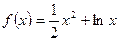
 为
为 的极值点,求实数
的极值点,求实数 的值
的值 是函数
是函数 的一个零点, 且
的一个零点, 且 , 其中
, 其中 , 则求
, 则求 的值
的值 时
时 ,求
,求 的取值范围
的取值范围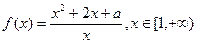 。
。 时,求函数
时,求函数 的最小值;
的最小值; >0恒成立,试求实数
>0恒成立,试求实数 的取值范围。
的取值范围。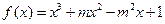 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.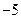 的直线是曲线
的直线是曲线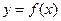 的切线,求此直线方程.
的切线,求此直线方程.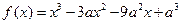 .
.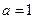 ,求函数
,求函数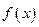 的极值;
的极值;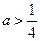 ,且当
,且当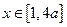 时,
时,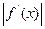
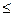 12a恒成立,试确定
12a恒成立,试确定 的取值范围.
的取值范围.