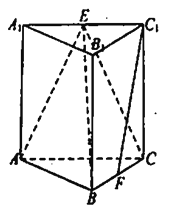
题目内容
【题目】已知椭圆C：
的离心率为
，右焦点
到直线
：
的距离为
．
Ⅰ
求椭圆C的方程；
Ⅱ过椭圆右焦点斜率为
的直线l与椭圆C相交于E、F两点，A为椭圆的右顶点，直线AE，AF分别交直线
于点M，N，线段MN的中点为P，记直线
的斜率为
，求证：
为定值．
【答案】（1）
．（2）证明见解析.
【解析】
试题（1）根据离心率为
，可得
之间的关系，再右焦点
到直线
的距离为
，就可求出的值，从而求出
的值（2）解决直线和椭圆的综合问题时注意：第一步：根据题意设直线方程，有的题设条件已知点，而斜率未知；有的题设条件已知斜率，点不定，可由点斜式设直线方程.第二步：联立方程：把所设直线方程与椭圆的方程联立，消去一个元，得到一个一元二次方程.第三步：求解判别式
：计算一元二次方程根.第四步：写出根与系数的关系.第五步：根据题设条件求解问题中结论.
试题解析：（Ⅰ）由题意得
，
， 2分
所以
，
，所求椭圆方程为． 4分
（Ⅱ）设过点
的直线
方程为：
，
设点
，点
， 5分
将直线方程代入椭圆
，
整理得：
6分
因为点
在椭圆内，所以直线和椭圆都相交，
恒成立，
且
7分
直线
的方程为：
，直线
的方程为：
令
，得点
，
，所以点的坐标
， 9分
直线
的斜率为
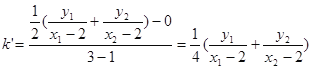
， 11分
将
代入上式得：
，
所以
为定值
． 13
小学学习好帮手系列答案
小学同步三练核心密卷系列答案【题目】某汽车公司对最近6个月内的市场占有率进行了统计，结果如表；
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合
与
之间的关系吗?如果能,请求出关于的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购
两款车扩大市场, 两款车各100辆的资料如表：
车型 | 报废年限（年） | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年，用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: 
，
，
，
.
参考公式:相关系数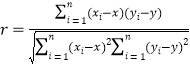
；
回归直线方程为
,其中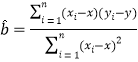
，
.
