题目内容
【题目】已知函数
，其中
．
（1）若
，求曲线
在点
处的切线方程；
（2）求
在
上的最小值．
【答案】（1）
；（2）
．
【解析】
（1）求出导数，当
时求出
、
，即可写出切线的点斜式方程；（2）求出
的两根，分析函数的单调性，分类讨论函数
在
上的单调性从而求最小值.
（1）的定义域为
，且
，
当时，
，
，
∴曲线
在点
处的切线方程为
，即．
（2）由，可知判别式为
，
令，得
或
，
和
的情况如下：
|
|
|
|
|
|
| + | 0 |
| 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
故的单调增区间为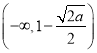
，
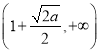；单调减区间为
，
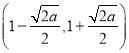①当
时，
，此时在上单调递增，
∴在上的最小值是
；
②当
时，
，此时在
上单调递减，在
上单调递增，
∴在上的最小值是
；
③当
时，
，此时在上单调递减，
∴在上的最小值是
．
综上所述，当时，在上的最小值是
；
当时，在上的最小值是
；
当时，在上的最小值是．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】为了调查微信用户每天使用微信的时间，某经销化妆品的店家在一广场随机采访男性、女性用户各50名，将男性、女性平均每天使用微信的时间（单位：
）分成5组：
，
，
，
，
分别加以统计，得到如图所示的频率分布直方图．
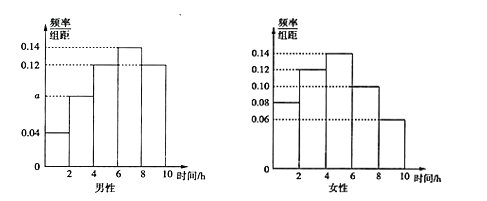
（1）根据男性的频率分布直方图，求
的值；
（2）①若每天玩微信超过
的用户称为“微信控”，否则称为“非微信控”，根据男性，女性频率分布直方图完成下面
列联表（不用写计算过程）
微信控 | 非微信 | 总计 | |
男性 | |||
女性 | |||
总计 | 100 |
②判断是否有90%的把握认为“微信控”与性别有关？说明你的理由．（下面独立性检验的临界值表供参考）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：
，其中
．
