题目内容
已知函数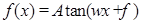
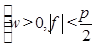 ,
,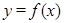 的部分图象如图所示,则
的部分图象如图所示,则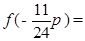 ( )
( )
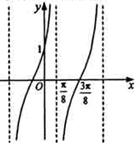
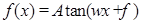
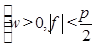 ,
,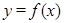 的部分图象如图所示,则
的部分图象如图所示,则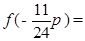 ( )
( )
A.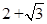 | B.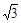 | C.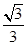 | D.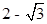 |
B
试题分析:根据题意,由于函数
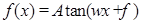
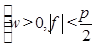 ,
,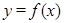 的部分图象可知函数的周期为
的部分图象可知函数的周期为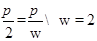 ,故可知将
,故可知将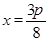 代入可知,函数值为零,则可知得到
代入可知,函数值为零,则可知得到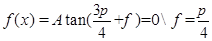 ,故可知由于过点(0,1)可知A=1,故可知解析式为
,故可知由于过点(0,1)可知A=1,故可知解析式为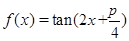 ,故
,故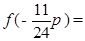
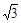 ,故答案为B.
,故答案为B.点评:主要考查了三角函数图象与性质的运用,属于基础题。

练习册系列答案
相关题目
题目内容
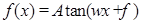
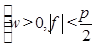 ,
,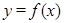 的部分图象如图所示,则
的部分图象如图所示,则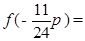 ( )
( )
A.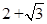 | B.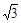 | C.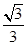 | D.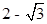 |
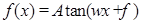
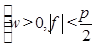 ,
,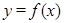 的部分图象可知函数的周期为
的部分图象可知函数的周期为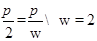 ,故可知将
,故可知将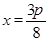 代入可知,函数值为零,则可知得到
代入可知,函数值为零,则可知得到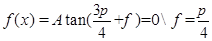 ,故可知由于过点(0,1)可知A=1,故可知解析式为
,故可知由于过点(0,1)可知A=1,故可知解析式为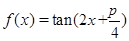 ,故
,故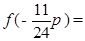
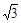 ,故答案为B.
,故答案为B.