题目内容
已知函数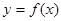 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时,
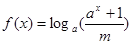 ,(
,( 。
。
(1)求实数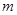 的值;并求函数
的值;并求函数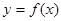 在定义域
在定义域 上的解析式;
上的解析式;
(2)求证:函数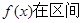
 上是增函数。
上是增函数。
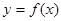 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时,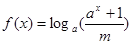 ,(
,( 。
。(1)求实数
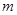 的值;并求函数
的值;并求函数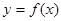 在定义域
在定义域 上的解析式;
上的解析式;(2)求证:函数
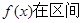
 上是增函数。
上是增函数。(1)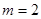 ,
,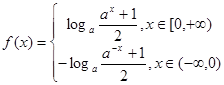
(2)利用定义法来作差变形定号下结论来得到证明。
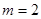 ,
,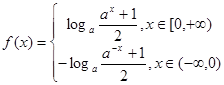
(2)利用定义法来作差变形定号下结论来得到证明。
试题分析:解:(1)
 函数
函数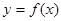 是定义域为
是定义域为 的奇函数,
的奇函数,∴
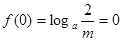 ∴
∴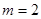 2分
2分当
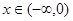 时,
时,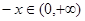 ,
,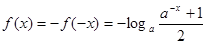 4分
4分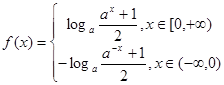 5分
5分(2)当
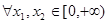 ,且
,且 ,
, 当
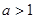 时,∵
时,∵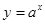 为增函数,∴
为增函数,∴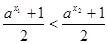
又
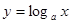 也为增函数,
也为增函数,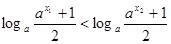 ,即
,即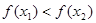
当
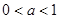 时,∵
时,∵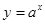 为减函数,∴
为减函数,∴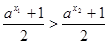
又
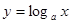 也为减函数,
也为减函数,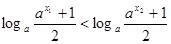 ,即
,即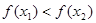
综上,都有
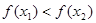 ,函数
,函数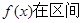
 上是增函数。10分
上是增函数。10分点评:主要是考查了函数的单调性的运用,属于中档题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
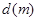 与车速
与车速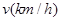 和车长
和车长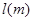 的关系满足:
的关系满足: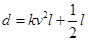 (
(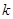 为正的常数),假定车身长为
为正的常数),假定车身长为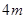 ,当车速为
,当车速为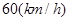 时,车距为2.66个车身长.
时,车距为2.66个车身长.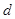 关于车速
关于车速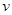 的函数关系式;
的函数关系式;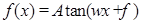
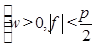 ,
,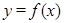 的部分图象如图所示,则
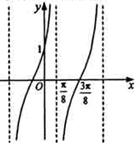
的部分图象如图所示,则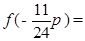 ( )
( )
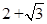
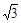
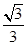
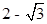
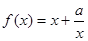 定义域为
定义域为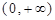 ,且
,且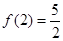 .设点
.设点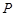 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点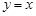 和
和 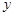 轴的垂线,垂足分别为
轴的垂线,垂足分别为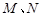 .
.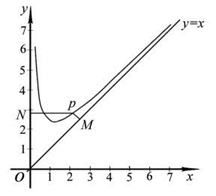
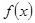 的单调递减区间(不必证明);
的单调递减区间(不必证明);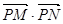 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;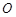 为坐标原点,求四边形
为坐标原点,求四边形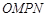 面积的最小值.
面积的最小值.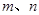 分别是方程
分别是方程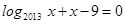 和
和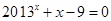 的根,则
的根,则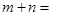
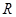 上的函数
上的函数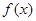 满足
满足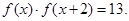 若
若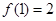 ,则
,则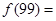 ( )
( )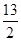
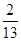
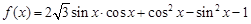 (
(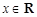 )
)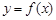 的周期和递增区间;
的周期和递增区间;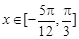 ,求
,求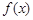 的取值范围.
的取值范围.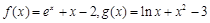 . 若实数a, b满足
. 若实数a, b满足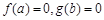 , 则( )
, 则( )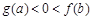
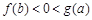

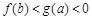
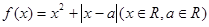 .
.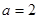 时,求
时,求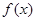 的单调区间;
的单调区间;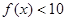 对
对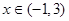 恒成立,求实数
恒成立,求实数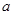 的取值范围.
的取值范围.