Question

10．若关于x的方程|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|-kx-1=0有五个互不相等的实根，则k的取值范围是（　　）

• A． （-$\frac{1}{4}$，$\frac{1}{4}$）
• B． （-∞，-$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞）
• C． （-∞，-$\frac{1}{8}$）∪（$\frac{1}{8}$，+∞）
• D． （-$\frac{1}{8}$，0）∪（0，$\frac{1}{8}$）

Answer 1

分析 方程|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|-kx-1=0，得到|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|=kx+1，设函数f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|，g（x）=kx+1，然后分别作出函数f（x）和g（x）的图象，利用图象确定k的取值范围

解答 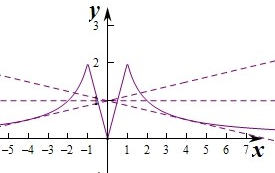解：∵方程|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|-kx-1=0，
∴|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|=kx+1，
设函数f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|，g（x）=kx+1，
则f（x）=$\left\{\begin{array}{l}{-\frac{2}{x}，x＜-1}\\{-2x，-1≤x≤0}\\{2x，0＜x＜1}\\{\frac{2}{x}，x≥1}\end{array}\right.$，
当x＞1时，由直线g（x）=kx+1与f（x）=$\frac{2}{x}$相切时，得kx+1=$\frac{2}{x}$，
即kx²+x-2=0，由△=1+4×2k=0，解得k=-$\frac{1}{8}$，
当x＜-1时，由直线g（x）=kx+1与f（x）=-$\frac{2}{x}$相切时，得kx+1=-$\frac{2}{x}$，
即kx²+x+2=0，由△=1-4×2k=0，解得k=$\frac{1}{8}$，
∴要使关于x的方程有五个互不相等的实根，
则由图象可知-$\frac{1}{8}$＜k＜0或0＜k＜$\frac{1}{8}$，
即k的取值范围是（-$\frac{1}{8}$，0）∪（0，$\frac{1}{8}$），
故选：D．

点评 本题主要考查方程根的个数的应用，利用方程和函数之间的关系，作出函数的图象，利用数形结合是解决本题的关键．综合性较强，难度较大