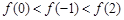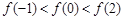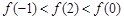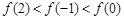题目内容
(本题满分12分)设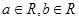 ,
,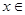
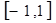 时,
时,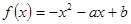 的最小值是-1,最大值是1,求
的最小值是-1,最大值是1,求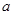 、
、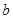 的值.
的值.
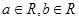 ,
,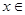
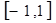 时,
时,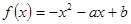 的最小值是-1,最大值是1,求
的最小值是-1,最大值是1,求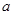 、
、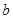 的值.
的值.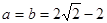 或
或 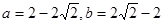 。
。本题考查了二次函数的最值,本题主要考查对 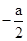 与x取值范围得讨论,比较复杂,有一定难度.
与x取值范围得讨论,比较复杂,有一定难度.
首先对该二次函数作出形状与性质的初步判断,该函数开口向上,求得对称轴,其次这是一个定区间(-1≤x≤1),对称轴(x=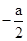 )的函数,所以需要对对称轴所在位置进行分类讨论.而求得。
)的函数,所以需要对对称轴所在位置进行分类讨论.而求得。
解: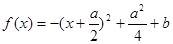
(1)若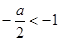 ,即
,即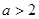 时, 则
时, 则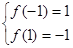 无解;
无解;
(2)若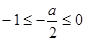 ,即
,即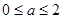 时,则
时,则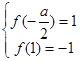 ,
,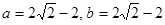 ;
;
(3)若 ,即
,即 时, 则
时, 则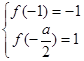 ,
,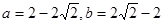 ;
;
(4)若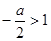 ,即
,即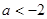 时, 则
时, 则 无解;
无解;
综上: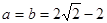 或
或 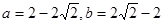
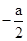 与x取值范围得讨论,比较复杂,有一定难度.
与x取值范围得讨论,比较复杂,有一定难度.首先对该二次函数作出形状与性质的初步判断,该函数开口向上,求得对称轴,其次这是一个定区间(-1≤x≤1),对称轴(x=
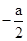 )的函数,所以需要对对称轴所在位置进行分类讨论.而求得。
)的函数,所以需要对对称轴所在位置进行分类讨论.而求得。解:
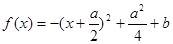
(1)若
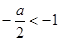 ,即
,即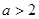 时, 则
时, 则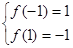 无解;
无解;(2)若
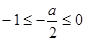 ,即
,即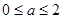 时,则
时,则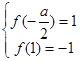 ,
,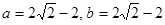 ;
;(3)若
 ,即
,即 时, 则
时, 则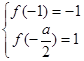 ,
,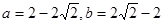 ;
;(4)若
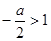 ,即
,即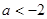 时, 则
时, 则 无解;
无解;综上:
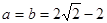 或
或 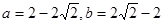

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
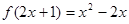 ,则
,则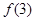 = .
= . 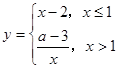 在R上单调递增,则实数
在R上单调递增,则实数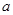 的取值范围是 ( )
的取值范围是 ( )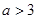
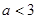
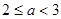
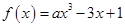 对于
对于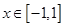 总有
总有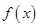 ≥0 成立,则
≥0 成立,则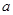 = .
= .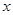 表示P点的行程,
表示P点的行程,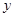 表示PA的长,求
表示PA的长,求 。
。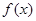 (
(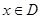 ),若存在两条距离为
),若存在两条距离为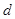 的直线
的直线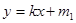 和
和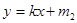 ,使得在
,使得在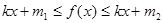 恒成立,则称函数
恒成立,则称函数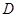 内有一个宽度为
内有一个宽度为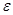 ,都存在一个实数
,都存在一个实数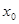 ,使得函数
,使得函数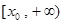 内有一个宽度为
内有一个宽度为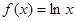 ,②
,②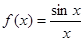 ,③
,③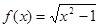 ,④
,④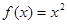 ,
,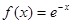 ,其中在正无穷处有永恒通道的函数的序号是_____________
,其中在正无穷处有永恒通道的函数的序号是_____________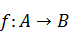 ,其中集合
,其中集合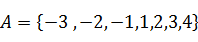 ,集合
,集合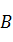 中的元素都是
中的元素都是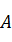 中元素在映射
中元素在映射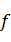 下的象,且对于任意的
下的象,且对于任意的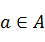 ,在
,在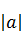 ,则集合
,则集合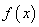 定义域为
定义域为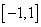 ,若对于任意的
,若对于任意的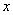 ,
,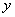
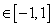 ,都有
,都有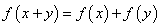 ,且
,且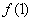 =1,若
=1,若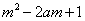 ,对所有
,对所有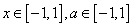 恒成立,求实数
恒成立,求实数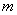 的取值范围.
的取值范围.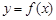 是偶函数,
是偶函数,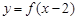 在[0,2]上是单调减函数,则( )
在[0,2]上是单调减函数,则( )