题目内容
已知函数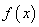 定义域为
定义域为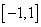 ,若对于任意的
,若对于任意的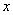 ,
,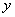
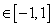 ,都有
,都有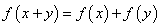 ,且
,且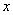 >0时,有
>0时,有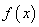 >0.
>0.
⑴证明: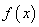 为奇函数;
为奇函数;
⑵证明: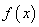 在
在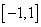 上为单调递增函数;
上为单调递增函数;
⑶设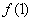 =1,若
=1,若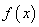 <
<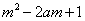 ,对所有
,对所有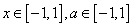 恒成立,求实数
恒成立,求实数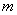 的取值范围.
的取值范围.
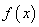 定义域为
定义域为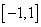 ,若对于任意的
,若对于任意的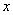 ,
,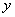
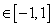 ,都有
,都有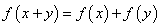 ,且
,且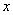 >0时,有
>0时,有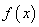 >0.
>0.⑴证明:
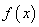 为奇函数;
为奇函数;⑵证明:
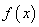 在
在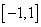 上为单调递增函数;
上为单调递增函数;⑶设
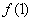 =1,若
=1,若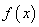 <
<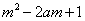 ,对所有
,对所有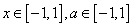 恒成立,求实数
恒成立,求实数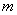 的取值范围.
的取值范围.(1)略
(2)略
(3)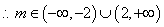
(2)略
(3)
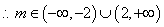
本试题主要考查了函数的奇偶性以及函数单调性的运用。
(1)通过合理的赋值,可知f(0),然后赋值得到f(x)和f(-x)的关系式得到证明。
(2)利用定义法证明函数的单调性。
(3)不等式的恒成立问题转化为函数的最值来求解得到
(1)通过合理的赋值,可知f(0),然后赋值得到f(x)和f(-x)的关系式得到证明。
(2)利用定义法证明函数的单调性。
(3)不等式的恒成立问题转化为函数的最值来求解得到

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
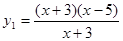 ,
,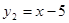
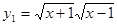 ,
,
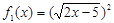 ,
,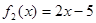
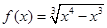 ,
,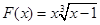
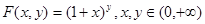 .
.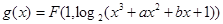 的图象为曲线
的图象为曲线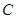 ,若存在实数
,若存在实数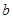 ,使得曲线
,使得曲线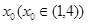 处有斜率是
处有斜率是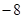 的切线,求实数
的切线,求实数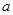 的取值范围;
的取值范围;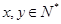 ,且
,且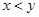 时,证明:
时,证明: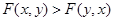 .
.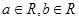 ,
,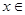
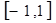 时,
时,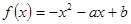 的最小值是-1,最大值是1,求
的最小值是-1,最大值是1,求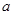 、
、 的值.
的值.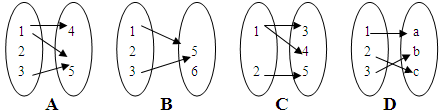
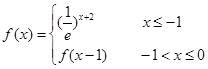 , 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )
, 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )
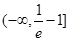
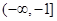
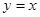 与
与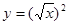
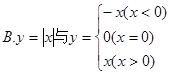
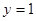 与
与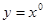
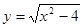 (x∈Z)与
(x∈Z)与 时单调递增,
时单调递增,
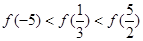
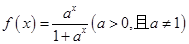 ,若用
,若用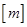 表示不超过实数
表示不超过实数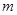 的最大整数,则函数
的最大整数,则函数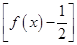
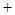
 的值域为_____________.
的值域为_____________.