题目内容
【题目】已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<![]() )一个周期内的图象上的四个点,如图所示,A(﹣
)一个周期内的图象上的四个点,如图所示,A(﹣![]() , 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
, 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,![]() 在x轴方向上的投影为
在x轴方向上的投影为![]() .
.
(1)求函数f(x)的解析式及单调递减区间;
(2)将函数f(x)的图象向左平移![]() 得到函数g(x)的图象,已知g(α)=
得到函数g(x)的图象,已知g(α)=![]() , α∈(﹣
, α∈(﹣![]() , 0),求g(α+
, 0),求g(α+![]() )的值.
)的值.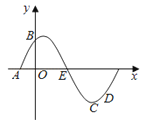
【答案】解:(1)∵如图所示,A(﹣![]() ,0),B为y轴上的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
,0),B为y轴上的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,![]() 在x轴上的投影为
在x轴上的投影为![]() ,
,
∴根据对称性得出:最大值点的横坐标为![]() ,
,
∴![]() =
=![]() +
+![]() ,T=π,
,T=π,
∵T=![]() ,
,
∴ω=2,
∵A(﹣![]() ,0)在函数图象上,
,0)在函数图象上,
∴sin(﹣![]() +φ)=0,解得:﹣
+φ)=0,解得:﹣![]() +φ=kπ,k∈z,可得:φ=kπ+
+φ=kπ,k∈z,可得:φ=kπ+![]() ,k∈z,
,k∈z,
∴φ=![]() ,故可得函数f(x)的解析式为:y=sin(2x+
,故可得函数f(x)的解析式为:y=sin(2x+![]() ).
).
∴由2kπ+![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z即可解得单调递减区间为:[kπ+
,k∈Z即可解得单调递减区间为:[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
(2)∵由题意可得:g(x)=f(x+![]() )=sin[2(x+
)=sin[2(x+![]() )+
)+![]() ]=sin(2x+
]=sin(2x+![]() )=cos2x.
)=cos2x.
∴g(α)=cos2α=![]() ,
,
∵α∈(﹣![]() ,0),
,0),
∴2α∈(﹣![]() ,0),可得sin2α=﹣
,0),可得sin2α=﹣![]() ,
,
∴g(α+![]() )=cos(2α+
)=cos(2α+![]() )=cos2αcos
)=cos2αcos![]() ﹣sin2αsin
﹣sin2αsin![]() =
=![]() x
x![]() ﹣(﹣
﹣(﹣![]() )×
)×![]() =
=![]() .
.
【解析】(1)根据函数想性质得出最大值点的横坐标为![]() , A(﹣
, A(﹣![]() , 0),得出周期T=π,T=
, 0),得出周期T=π,T=![]() , 即可ω,运用A(﹣
, 即可ω,运用A(﹣![]() , 0),sin(﹣
, 0),sin(﹣![]() +φ)=0,得出φ=
+φ)=0,得出φ=![]() kπ+
kπ+![]() , k∈z,即可求解函数解析式,由2kπ+
, k∈z,即可求解函数解析式,由2kπ+![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() , k∈Z即可解得单调递减区间.
, k∈Z即可解得单调递减区间.
(2)利用函数y=Asin(ωx+φ)的图象变换可求g(x),结合角的范围可求cos2α,sin2α,利用两角和的余弦函数公式即可求值。
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.