题目内容
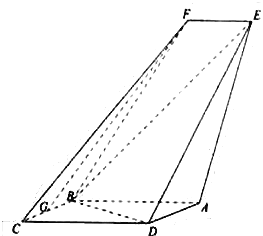
【题目】如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
(I)用t表示出PQ的长度,并探求△CPQ的周长l是否为定值;
(Ⅱ)设探照灯照射在正方形ABCD内部区域的面积S(平方百米),求S的最大值.
【答案】解:(Ⅰ)由BP=t,得CP=1﹣t,0≤t≤1,
设∠PAB=θ,
则∠DAQ=45°﹣θ,
DQ=tan(45°﹣θ)=![]() ,CQ=1﹣
,CQ=1﹣![]() =
=![]() ,
,
∴PQ=![]() =
=![]() =
=![]() ,
,
∴l=CP+CQ+PQ=1﹣t+![]() +
+![]() =1﹣t+1+t=2,是定值
=1﹣t+1+t=2,是定值
(Ⅱ)S=S正方形ABCD﹣S△ABP﹣S△ADQ=1×1﹣![]() ×1×t﹣
×1×t﹣![]() ×1×
×1×![]() ,
,
=1﹣![]() t﹣
t﹣![]()
![]() =1﹣
=1﹣![]() t﹣
t﹣![]() (﹣1+
(﹣1+![]() ),
),
=1+![]() ﹣
﹣![]() ﹣
﹣![]() ,
,
=2﹣(![]() +
+![]() ),
),
由于1+t>0,
则S=2﹣(![]() +
+![]() )≤2﹣2
)≤2﹣2![]() =2﹣
=2﹣![]() ,当且仅当
,当且仅当![]() =
=![]() ,即t=
,即t=![]() ﹣1时等号成立,
﹣1时等号成立,
故探照灯照射在正方形ABCD内部区域的面积S最多为2﹣![]() 平方百米.
平方百米.
【解析】(Ⅰ)由BP=t,得CP=1﹣t,0≤t≤1,设∠PAB=θ,则∠DAQ=45°﹣θ,分别求出CP,CQ,PQ即可得到求出周长l=2,问题得以解决;
(Ⅱ)根据S=S正方形ABCD﹣S△ABP﹣S△ADQ得到S=2﹣(![]() +
+![]() ),根据基本不等式的性质即可求出S的最大值。
),根据基本不等式的性质即可求出S的最大值。

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目