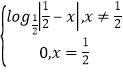Question

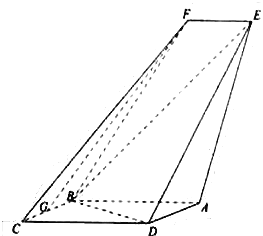
【题目】如图，某自行车手从O点出发，沿折线O﹣A﹣B﹣O匀速骑行，其中点A位于点O南偏东45°且与点O相距20 千米．该车手于上午8点整到达点A，8点20分骑至点C，其中点C位于点O南偏东（45°﹣α）（其中sinα= ，0°＜α＜90°）且与点O相距5 千米（假设所有路面及观测点都在同一水平面上）．

（1）求该自行车手的骑行速度；

（2）若点O正西方向27.5千米处有个气象观测站E，假定以点E为中心的3.5千米范围内有长时间的持续强降雨．试问：该自行车手会不会进入降雨区，并说明理由．

Answer 1

【答案】（1）（2）会进入

【解析】

（1）根据余弦定理可求出AC的长，从而可求出自行车的速度；

（2）先根据余弦定理求出cos∠OAC，再根据正弦定理可得OM，再在Rt△EHM中，求出EM的大小，比较后即可得到结论．

（1）由题意知：OA=2，OC， ∠AOC=α，sinα=．

由于0°＜α＜90°，

所以．

在△AOC中，由余弦定理得

，

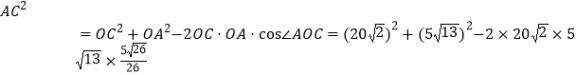
所以，

所以该自行车手的行驶速度为（千米/小时）．

（2）如图，

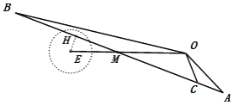
设直线OE与AB相交于点M．

在△AOC中，由余弦定理得

cos∠OAC

从而 sin∠OAC．

在△AOM中，由正弦定理得，

所以，

由于OE=27.5＞40=OM，

所以点M位于点O和点E之间，且ME=OE﹣OM=7.5．

过点E作EH AB于点H，

则EH为点E到直线AB的距离．

在Rt△EHM中，EH=EMsin∠EMH=EMsin（45°﹣∠OAC）．

所以该自行车手会进入降雨区．