题目内容
19．设函数g（x）=1+x且当x≠0时，f（g（x））=$\frac{1-x}{x}$，则f（$\frac{1}{2}$）=（ ）| A． | 0 | B． | 1 | C． | 3 | D． | -3 |
分析 令g（x）=1+x=$\frac{1}{2}$，则x=-$\frac{1}{2}$，结合f（g（x））=$\frac{1-x}{x}$，代入可得答案．
解答 解：令g（x）=1+x=$\frac{1}{2}$，
则x=-$\frac{1}{2}$，
∵f（g（x））=$\frac{1-x}{x}$，
∴f（$\frac{1}{2}$）=$\frac{1-（-\frac{1}{2}）}{-\frac{1}{2}}$=-3，
故选：D
点评 本题考查的知识点是函数的值，难度不大，属于基础题．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
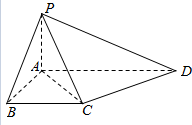如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，AD⊥AB，BC∥AD，AD=2AB=2BC=2．求证：PC⊥CD．
14．已知圆的方程为x2+y2+2x=0则该圆的半径为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
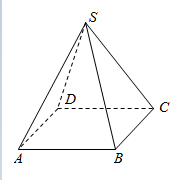如图，在正四棱锥S-ABCD中，底面边长为6cm，侧棱长为3$\sqrt{5}$cm．