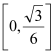Question

【题目】已知函数，

(1)若的一个极值点到直线的距离为1，求的值；

(2)求方程的根的个数

Answer 1

【答案】（1）a＝－2或a＝－8.（2）见解析

【解析】试题分析：（1）先求出函数 的导函数 ，令，可得函数只有一个极值点，根据点到直线的距离公式可得结果；（2） 根的个数等价于的零点个数，利用导数研究函数的单调性，可得结果.

试题解析：(1)由f′(x)＝＝0，得x＝0，

故f(x)仅有一个极小值点M(0,0)，

根据题意得：

d＝＝1.

∴a＝－2或a＝－8.

(2)令h(x)＝f(x)－g(x)＝ln(x2＋1)－－a，

h′(x)＝＋＝2x.

当x∈(0,1)∪(1，＋∞)时，h′(x)≥0，

当x∈(－∞，－1)∪(－1,0)时，h′(x)＜0.

因此，h(x)在(－∞，－1)，(－1,0)上时，h(x)单调递减，

在(0,1)，(1，＋∞)上时，h(x)单调递增.

又h(x)为偶函数，当x∈(－1,1)时，h(x)的极小值为h(0)＝1－a.

当x→－1－时，h(x)→－∞，当x→－1＋时，h(x)→＋∞，

当x→－∞时，h(x)→＋∞，当x→＋∞时，h(x)→＋∞.

由根的存在性定理知，方程在(－∞，－1)和(1，＋∞)一定有根

故f(x)＝g(x)的根的情况为：

当1－a＞0时，即a＜1时，原方程有2个根；

当1－a＝0时，即a＝1时，原方程有3个根．

当1－a<0时，即a>1时，原方程有4个根．