题目内容
【题目】已知函数![]()
(1)若![]() ,且
,且![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围
的取值范围
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)实数
;(2)实数![]() 是存在的,且
是存在的,且![]() .
.
【解析】
试题分析:(1)原题等价于![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 恒成立,分离参数得
恒成立,分离参数得![]() ,只需求得函数
,只需求得函数![]() 在区间
在区间![]() 值域即可;
值域即可;
(2)利用反证法假设存在这样的实数![]() ,则
,则![]() 在
在![]() 时恒成立,且可以取到等号,故
时恒成立,且可以取到等号,故![]() ,即
,即![]() ,利用导函数求得函数
,利用导函数求得函数![]() 的最小值,最后令最小值等于1,可求出参数
的最小值,最后令最小值等于1,可求出参数![]() 的范围.
的范围.
试题解析:(1)![]()
由已知![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 恒成立
恒成立
分离参数得![]() ,
,
因为![]()
所以![]()
所以正实数![]() 的取值范围为:
的取值范围为:![]()
(2)假设存在这样的实数![]() ,则
,则![]() 在
在![]() 时恒成立,且可以取到等号
时恒成立,且可以取到等号
故![]() ,即
,即![]()
从而这样的实数![]() 必须为正实数,当
必须为正实数,当![]() 时,由上面的讨论知
时,由上面的讨论知![]() 在
在![]() 上递增,
上递增,![]() ,此时不合题意,故这样的
,此时不合题意,故这样的![]() 必须满足
必须满足![]() ,此时:
,此时:
令![]() 得
得![]() 的增区间为
的增区间为![]()
令![]() 得
得![]() 的减区间为
的减区间为![]()
故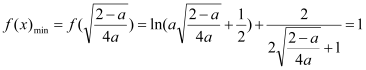
整理得
即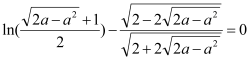 ,设
,设![]() ,
,
则上式即为![]() ,构造
,构造![]() ,则等价于
,则等价于![]()
由于![]() 为增函数,
为增函数,![]() 为减函数,故
为减函数,故![]() 为增函数
为增函数
观察知![]() ,故
,故![]() 等价于
等价于![]() ,与之对应的
,与之对应的![]()
综上符合条件的实数![]() 是存在的,且
是存在的,且![]()

练习册系列答案
相关题目
【题目】重庆市某厂党支部10月份开展“两学一做”活动,将10名党员技工平均分为甲,乙两组进行技能比赛.要求在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.
