题目内容
【题目】四棱锥P﹣ABCD中,PA⊥底面ABCD,且PA=AB=AD=![]() CD,AB∥CD,∠ADC=90°.
CD,AB∥CD,∠ADC=90°.
(1)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论;
(2)求证:平面PBC⊥平面PCD;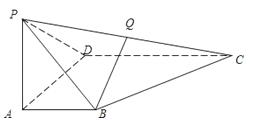
【答案】
解:(1)当Q为侧棱PC中点时,有BQ∥平面PAD.
证明如下:如图,取PD的中点E,连AE、EQ.
∵Q为PC中点,则EQ为△PCD的中位线,
∴EQ∥CD且EQ=![]() CD.
CD.
∵AB∥CD且AB=![]() CD,∴EQ∥AB且EQ=AB,
CD,∴EQ∥AB且EQ=AB,
∴四边形ABQE为平行四边形,则BQ∥AE.
∵BQ平面PAD,AE平面PAD,
∴BQ∥平面PAD.
(2)证:∵PA⊥底面ABCD,∴PA⊥CD.
∵AD⊥CD,PA∩AD=A,∴CD⊥平面PAD.
∵AE平面PAD,∴CD⊥AE.
∵PA=AD,E为PD中点,∴AE⊥PD.
∵CD∩PD=D,∴AE⊥平面PCD.
∵BQ∥AE,∴BQ⊥平面PCD.
∵BQ平面PBC,∴平面PBC⊥平面PCD.
【解析】(1)当Q为侧棱PC中点时,有BQ∥平面PAD.取PD的中点E,连AE、EQ.只需证明平面PAD外的直线BQ平行于平面PAD内的直线AE,即可.
(2)要证平面PBC⊥平面PCD,只需证明AE垂直平面PAD内的两条相交直线CD、PD,BQ∥AE,BQ平面PBC即可;
【考点精析】掌握直线与平面平行的性质和平面与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;一个平面过另一个平面的垂线,则这两个平面垂直.

 名校课堂系列答案
名校课堂系列答案【题目】在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:
分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
频数 | 1 | 2 | 6 | 7 | 3 | 1 |
分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为( )
A.10%
B.20%
C.30%
D.40%