题目内容
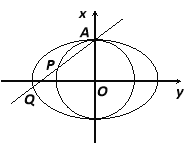
【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图，在平面直角坐标系
中，已知椭圆
的离心率为
，且右焦点
到左准线的距离为
．
（1）求椭圆
的标准方程；
（2）设
为椭圆
的左顶点，
为椭圆
上位于
轴上方的点，直线
交
轴于点
，过点
作
的垂线，交轴于点
．
（ⅰ）当直线的斜率为
时，求
的外接圆的方程；
（ⅱ）设直线
交椭圆于另一点
，求
的面积的最大值．
【答案】见解析
【解析】（1）由题意，得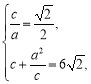
解得
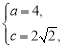则
，
所以椭圆
的标准方程为
．………………………………………4分
（2）由题可设直线
的方程为
，
，则
，
所以直线
的方程为
，则
．
(i)当直线的斜率为
，即
时，
，
，
，
因为
，所以圆心为
，半径为
，
所以
的外接圆的方程为
．……………………………8分
(ii)联立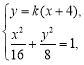
消去
并整理得，
，
解得
或
，所以
，……………………10分
直线
的方程为
，同理可得，
，
所以
，
关于原点对称，即
过原点．
所以
的面积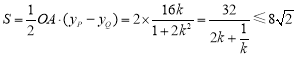
，……14分
当且仅当
，即
时，取“
”．
所以
的面积的最大值为
．…………………………………………16分
练习册系列答案
相关题目
【题目】【2017北京西城区5月模拟】某大学为调研学生在
，
两家餐厅用餐的满意度，从在
，
两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分.
整理评分数据，将分数以10为组距分成6组：
，
，
，
，
，
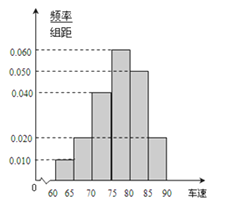
，得到
餐厅分数的频率分布直方图，和
餐厅分数的频数分布表：
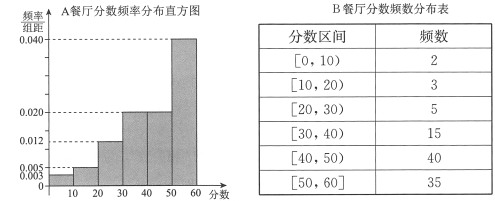
定义学生对餐厅评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 |
|
|
|
（Ⅰ）在抽样的100人中，求对
餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在
，
两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对
餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从
，
两家餐厅中选择一家用餐，你会选择哪一家？说明理由.
