题目内容
【题目】已知正数数列{an}的前n项和为Sn , 点P(an , Sn)在函数f(x)= ![]() x2+
x2+ ![]() x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
(1)求数列{an}的通项公式;
(2)若cn=anbn , 求数列{cn}的前n项和Tn;
(3)是否存在整数m,M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9,说明理由.
【答案】
(1)解:∵点P(an,Sn)在函数f(x)= ![]() x2+
x2+ ![]() x上,
x上,
∴Sn= ![]()
![]() +
+ ![]() an,Sn﹣1=
an,Sn﹣1= ![]()
![]() +
+ ![]() an﹣1(n≥2),
an﹣1(n≥2),
两式相减,整理得:(an+an﹣1)(an﹣an﹣1﹣1)=0,
又∵an>0,
∴an=an﹣1+1,
又∵S1= ![]()
![]() +
+ ![]() a1,即a1=1,
a1,即a1=1,
∴数列{an}是首项和公差均为1的等差数列,
∴an=n;
(2)解:∵b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
∴数列{bn}是首项为1、公比为 ![]() 的等比数列,
的等比数列,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
![]() Tn=
Tn= ![]() +2×
+2× ![]() +…+n×
+…+n× ![]() ,
,
两式相减,得: ![]() Tn=1+
Tn=1+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣n×
﹣n× ![]()
= ![]() ﹣n×
﹣n× ![]()
=3﹣(n+3)× ![]() ,
,
∴Tn=9﹣(3n+9)× ![]()
(3)解:结论:假设存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9.
理由如下:
由(2)知:Tn=9﹣(3n+9)× ![]() <9,
<9,
又∵Tn﹣1=9﹣[3(n﹣1)+9]× ![]() ,
,
∴Tn﹣Tn﹣1=(3n+6)× ![]() ﹣(3n+9)×
﹣(3n+9)× ![]() =n×
=n× ![]() >0,
>0,
∴数列{Tn}是单调递增数列,
∴(Tn)min=T1=9﹣12× ![]() =1,
=1,
∴1<Tn<9,
∴m=0,M=9,
∴存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9.
【解析】(1)通过将点P(an , Sn)代入函数f(x)= ![]() x2+
x2+ ![]() x中,利用Sn=
x中,利用Sn= ![]()
![]() +
+ ![]() an与Sn﹣1=
an与Sn﹣1= ![]()
![]() +
+ ![]() an﹣1(n≥2)作差,进而可知数列{an}是首项和公差均为1的等差数列,计算即得结论;(2)利用错位相减法计算即得结论;(3)通过(2)知Tn<9,利用作差法可知数列{Tn}是单调递增数列,进而计算可得结论.
an﹣1(n≥2)作差,进而可知数列{an}是首项和公差均为1的等差数列,计算即得结论;(2)利用错位相减法计算即得结论;(3)通过(2)知Tn<9,利用作差法可知数列{Tn}是单调递增数列,进而计算可得结论.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系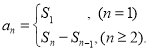 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如表:
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
资金 | 单位产品所需资金(百元) | ||
空调机 | 洗衣机 | 月资金供应量(百元) | |
成本 | 30 | 20 | 300 |
劳动力(工资) | 5 | 10 | 110 |
单位利润 | 6 | 8 | |
【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 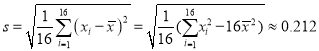 ,
, 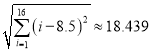 ,
, ![]() ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若
,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若![]() ,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在![]() 之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本![]()
![]() 的相关系数
的相关系数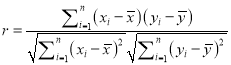 ,
, ![]() .
.